算法提高课汇总

次小生成树

参考 AcWing 1148. 秘密的牛奶运输 中的思路$2$:

• 枚举非树边$e’\notin T$, 加入$e’$后图中形成环$C$, 在环$C$中去掉一个树边$e$. 则新的生成树树权为
  $W(T) + W(e’) - W(e)$. 为使新生成树的树权最小, 我们需要找环$C$中边权最大的树边;
  然而由于题目求严格次小, 若最大边权$W(e) == W(e’)$, 则不满足条件. 此时我们还需要
  求环$C$上严格次大边权.

在AcWing 1148中我们通过$dfs$方式枚举从顶点$u$出发到顶点$v$的路径上边权的最大值以及严格次大边权值.

这里考虑用倍增$LCA$算法优化路径$u\rightarrow v$上最大以及严格次大边权值的查询时间.

倍增法优化

考虑任意两点$u, v$的路径:

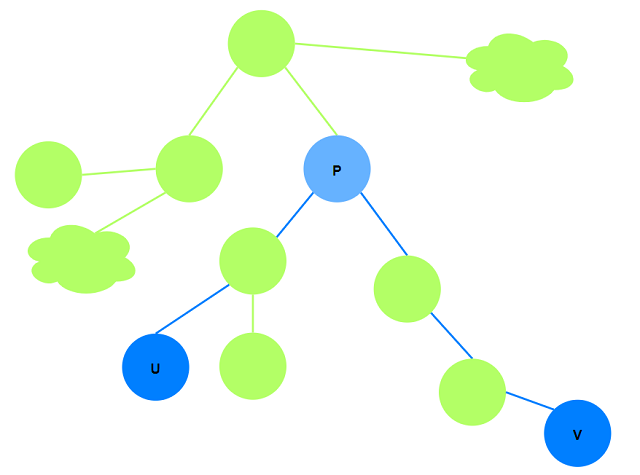
假设$u, v$的最近公共祖先为$p$, 则$u\rightarrow v$的路径可以分为独立的两个部分: $u\rightarrow p$以及$v\rightarrow p$.

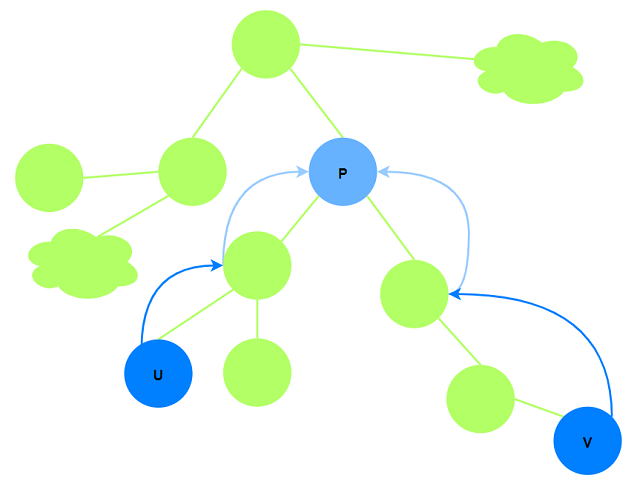
参考 AcWing 1172. 祖孙询问 我们知道可以通过倍增思路从$u$跳至$p$, $v$到$p$同理. 如果在跳的过程可以
得到跳跃路径经过所有边的最大边权以及严格次大边权值, 则综合两个独立路径我们就能得到$u\rightarrow v$
上的最大以及次大边权值, 每次查询的时间降至$\lg(n)$.

具体实现

• 加入状态$d1(u, i), d2(u, i)$: 类似倍增法代码中的$fa(u, i)$的含义, 从节点$u$向上走$2^i$步的路径
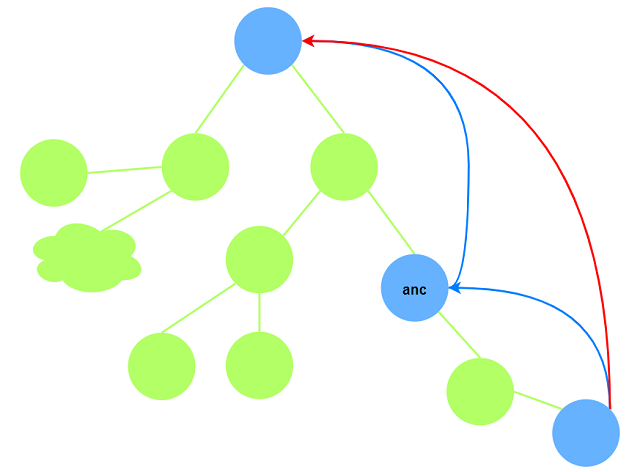
  上边权的最大值, 严格次大值.

  计算方式, 同样与$fa(u, i)$类似, 递推方式分两步计算: $u$向上$2^{i-1}$步路径上的最大与次大, 以及
  假设$u$向上$2^{i-1}$步到达节点$anc$, 再计算$anc$向上$2^{i-1}$步的最大与次大, 综合两步计算的结果.
  (类似$DP$思想, 之前的状态已经计算过了)
  

• 注意: 对于$u\rightarrow p$与$v\rightarrow p$路径计算, 在倍增法中节点向上跳至$p$的下一层就会
  停止, 最后需要额外考虑两节点向上1步路径的最大值(只有一步所以没有次大值);
  在向上过程中路径最大长度为$\lg(N)$, 两条路径即$2\times \lg(N)$, 而Y总开了$2\times N$当然也是正确的.

实现代码 $m\lg(m) + m\lg(n)$

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10, lgN = 16, E = 2 * N, M = 3e5 + 10, INF = 0x3f3f3f3f;
const ll LL_INF = 1e18;

int n, m;
int h[N], e[E], w[E], ne[E], idx; //存储最小生成树
int q[N], p[N]; //q: bfs中的队列; p: kruskal中的并查集
int depth[N], fa[N][lgN + 1], d1[N][lgN + 1], d2[N][lgN + 1];
struct Edge
{
    int u, v, w;
    bool used;
    bool operator< (const Edge &edge)
    {
        return w < edge.w;
    }
}edges[M];

void add(int u, int v, int c)
{
    e[idx] = v, w[idx] = c, ne[idx] = h[u], h[u] = idx ++;
}

int find(int x)
{
    return x == p[x] ? x : p[x] = find( p[x] );
}

ll kruskal()
{
    sort(edges, edges + m);
    for( int i = 1; i <= n; i ++ )  p[i] = i;

    ll sum = 0;
    for( int i = 0; i < m; i ++ )
    {
        int u = find( edges[i].u ), v = find( edges[i].v ), w = edges[i].w;
        if( u != v )
        {
            p[u] = v;
            sum += w;
            edges[i].used = true;
        }
    }
    return sum;
}

void build()
{
    memset(h, -1, sizeof h);
    for( int i = 0; i < m; i ++ )
    {
        if( edges[i].used )
        {
            int u = edges[i].u, v = edges[i].v, w = edges[i].w;
            add(u, v, w), add(v, u, w);
        }
    }
}

void bfs(int root)
{
    memset( depth, 0x3f, sizeof depth);
    depth[0] = 0; //depth[NULL] = 0
    depth[root] = 1;
    int hh = 0, tt = 0;
    q[tt ++] = root;

    while( hh < tt ) //从根向下按层遍历
    {
        int u = q[hh ++];

        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( depth[v] > depth[u] + 1 )
            {
                depth[v] = depth[u] + 1;
                q[tt ++] = v;

                fa[v][0] = u;
                d1[v][0] = w[i]; //v向上路径长度为1的边权最大 即u->v向上路径
                d2[v][0] = -INF; //路径长度为1 不存在次大

                for( int k = 1; k <= lgN; k ++ )
                {
                    int anc = fa[v][k - 1]; //递推 类似dp过程
                    fa[v][k] = fa[anc][k - 1];
                    //分两步考虑
                    int distance[] = {d1[v][k - 1], d2[v][k - 1], d1[anc][k - 1], d2[anc][k - 1]};
                    d1[v][k] = d2[v][k] = -INF;
                    for( int j = 0; j < 4; j ++ )
                    {
                        int d = distance[j];
                        if( d > d1[v][k] )  d2[v][k] = d1[v][k], d1[v][k] = d;
                        else if( d != d1[v][k] && d > d2[v][k] )    d2[v][k] = d;
                    }
                }
            }
        }
    }
}

int lca(int u, int v, int w)
{
    int cnt = 0;
    static int distance[2 * lgN]; //存储路径中的最大与次大边权

    if( depth[u] < depth[v] )   swap(u, v);

    for( int k = lgN; k >= 0; k -- )
    {
        if( depth[ fa[u][k] ] >= depth[v] )
        {
            distance[cnt ++] = d1[u][k]; //u -> fa[u][k]路径中的最大边权
            distance[cnt ++] = d2[u][k]; //u -> fa[u][k]路径中的次大边权
            u = fa[u][k];
        }
    }
    if( u != v )
    {
        for( int k = lgN; k >= 0; k -- )
        {
            if( fa[u][k] != fa[v][k] )
            {
                distance[cnt ++] = d1[u][k];
                distance[cnt ++] = d2[u][k];
                distance[cnt ++] = d1[v][k];
                distance[cnt ++] = d2[v][k];

                u = fa[u][k], v = fa[v][k];
            }
        }
        //最后u,v停在最近公共祖先的下一层 所以还要向上考虑一步
        distance[cnt ++] = d1[u][0];
        distance[cnt ++] = d1[v][0]; 
        //这里因为只有一步 不存在次大(-INF) 不用考虑
    }

    int dist1 = -INF, dist2 = -INF;
    for( int i = 0; i < cnt; i ++ )
    {
        int d = distance[i];
        if( d > dist1 ) dist2 = dist1, dist1 = d;
        else if( d != dist1 && d > dist2 )  dist2 = d;
    }

    if( w > dist1 ) return w - dist1;
    if( w > dist2 ) return w - dist2;
    return INF;  //return w - (-INF);
}

int main()
{
    scanf("%d%d", &n, &m);
    for( int i = 0; i < m; i ++ )
    {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        edges[i] = {u, v, w};
    }

    ll sum = kruskal();
    build(); //建立最小生成树
    bfs(1); //预处理depth[]; fa[][]; d1[][]; d2[][]

    ll res = LL_INF;
    for( int i = 0; i < m; i ++ )
        if( !edges[i].used )
        {//非树边
            int u = edges[i].u, v = edges[i].v, w = edges[i].w;
            res = min( res, sum + lca(u, v, w) );
        }
    printf("%lld\n", res);

    return 0;
}