Acwing2014. 岛

题目

每当下雨时，农夫约翰的田地总是被洪水淹没。

由于田地不是完全水平的，所以一些地方充满水后，留下了许多被水隔开的“岛”。

约翰的田地被描述为由 N 个连续高度值 H1,…,HN 指定的一维场景。

假设该场景被无限高的围墙包围着，请考虑暴雨期间发生的情况：

最低处首先被水覆盖，形成一些不连贯的岛，随着水位的不断上升，这些岛最终都会被覆盖。

一旦水位等于一块田地的高度，那块田地就被认为位于水下。

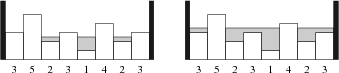
上图显示了一个示例：在左图中，我们只加入了刚好超过 11 单位的水，此时剩下 4 个岛（最大岛屿剩余数量），而在右图中，我们共加入了 7 单位的水，此时仅剩下 2 个岛。

请计算，暴风雨期间我们能在某个时间点看到的最大岛屿数量。

水会一直上升到所有田地都在水下。

输入格式

第一行包含整数 N。

接下来 N 行，每行包含一个整数表示 Hi。

输出格式

输出暴风雨期间我们能在某个时间点看到的最大岛屿数量。

数据范围

1≤N≤105,
1≤Hi≤109

输入样例：

8
3
5
2
3
1
4
2
3

输出样例：

4

为什么想到用差分(个人认为很重要)

AcWing 2014. 岛深入剖析差分的本质探究差分解法的由来 - AcWing

思路

设一块长方形的高度为a[i],假设水从a[i-1]涨到(下降到)a[i],意味着所有高度在a[i]—a[i-1]的长方形都会被淹没(露出来)，相当于这些长方形的高度差被抹平(产生)(对答案的贡献都减1(+1)).同时给一个区间减去(加上)一个数，用差分

4007. 非零段划分 - AcWing题库代码：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 500005,M = 10000;
int a[N],b[N];
int n;
int main()
{
    cin >> n;
    int res = 0;
    for (int i = 1; i <= n; i ++ ){
        cin >> a[i];
        if(a[i]>a[i-1]){
            //数的大小在[a[i-1],a[i]-1]之间的所有数都+1
            b[a[i-1]]++,b[a[i]]--;
        }
    }
    int sum = 0 ;
    for (int i = 0; i <= M; i ++ ){
        sum+=b[i];
        res = max(res,sum);
    }
    cout << res;
}

题解

对比4007. 非零段划分 - AcWing题库发现高度的数据范围比数量大的多余数想到了用map离散化(不能用unordered_map，unordered_map无法用来求前缀和)

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>


typedef long long LL;

using namespace std;
const int N = 100005,M = 1e9+1;
int a[N];
map<int ,int >b;
int n;
int main()
{
    cin >> n;

    for (int i = 1; i <= n; i ++ ){
        cin >> a[i];
        if(a[i]>a[i-1]){
            //数的大小在[a[i-1],a[i]-1]之间的所有数大小都+1
            b[a[i-1]]++,b[a[i]]--;
        }
    }
    LL sum = 0 ,res = 0;
    for (auto i:b ){
        //求前缀和
        sum+=i.second;
        res = max(res,sum);
    }
    cout << res;
}