耍杂技的牛

思路分析

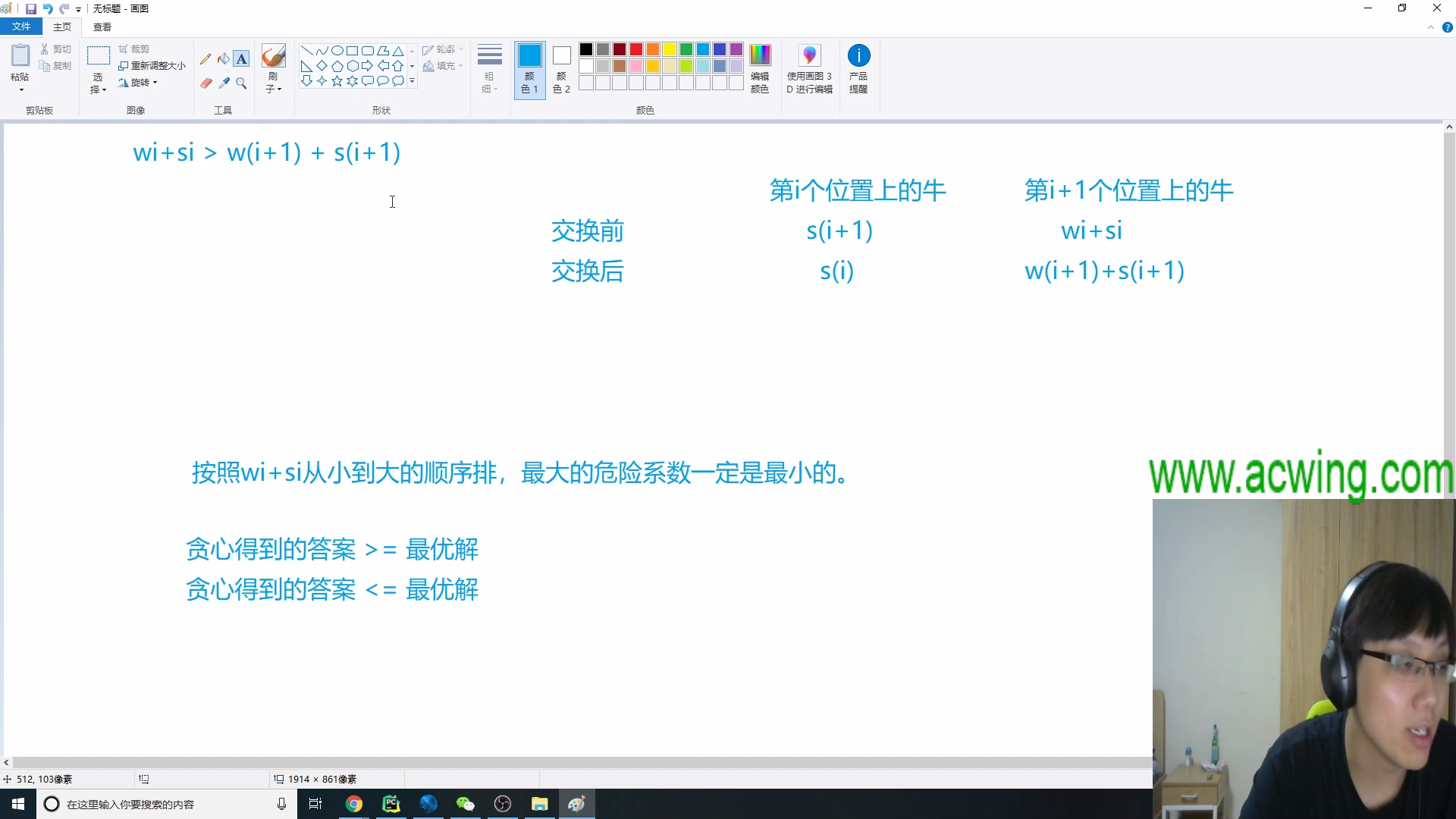
我们按(w + s)的值升序排列，值最小的在最上面，如此堆叠可得最优解

证明

我们只考虑相邻逆序的简单情况，这种情况是不会影响到其它的牛。并且任何一个逆序对优化，都可以通过调整转化成一个或多个相邻逆序的优化问题，来排除其它因素的干扰。

这里继续采用反证法，假设相邻两头牛逆序更好，也就是
$(w[i]$ $+$ $s[i])$ $>$ $(w[i + 1]$ $+$ $s[i + 1])$
这里讨论的是第$i$头牛与第$(i + 1)$头牛，之前重量和是$sum$

交换前  res = max(sum - s[i], sum + w[i] - s[i + 1])
交换后  res = max(sum - s[i + 1], sum + w[i + 1] - s[i])

同时(-sum + s[i] + s[i + 1])
得

交换前  res = max(s[i + 1], w[i] + s[i])
交换后  res = max(s[i], w[i + 1] + s[i + 1])

又已知$(w[i]$ $+$ $s[i])$ $>$ $(w[i + 1]$ $+$ $s[i + 1])$
且$w[i]$ $+$ $s[i]$ $>$ $s[i]$

也就是说交换前最大值比交换后的最大值大，更危险，与假设矛盾

所以$(s$ $+$ $w)$越小越好，放在上面，所以我们按它升序排列

代码

#include <iostream>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 50010;

int n;
PII cow[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        int s, w;
        scanf("%d%d", &w, &s);
        cow[i] = {w + s, w};
    }

    sort(cow, cow + n); // 排序

    int res = -2e9, sum = 0;
    for (int i = 0; i < n; i ++ )
    {
        int s = cow[i].first - cow[i].second, w = cow[i].second; // 从对组里面求出当前s和w
        res = max(res, sum - s); // 求答案
        sum += w; // 求sum
    }

    printf("%d\n", res);

    return 0;
}