算法提高课汇总

最近公共祖先 $Least\;Common\;Ancestor, LCA$

什么是最近公共祖先

在一颗有根树中, 每个节点向上追溯都有一系列祖宗节点. 对于任意两个节点, 在它们祖宗节点的交集
中离它们最近的节点称为它们的最近公共祖先.

注意: 节点本身也可作为其祖先节点.

最近公共祖先算法

$1.\;$向上标记法

算法步骤: 先从一个点向根遍历并标记其祖先节点, 再从另一个点向根遍历其祖先节点, 遇到第一个被标记
的节点即它们的最近公共祖先.

时间复杂度: 每次询问的时间复杂度为$O(n)$.

$2.\;$倍增法

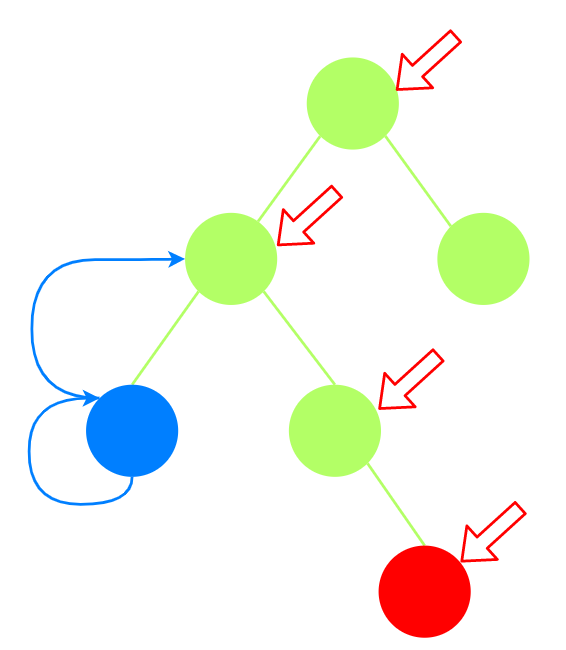
倍增法: 按$2$的倍数增大: $1, 2, 4, 8, …$ 也可以按从大到小的顺序$8, 4, 2, 1, …$

预处理:

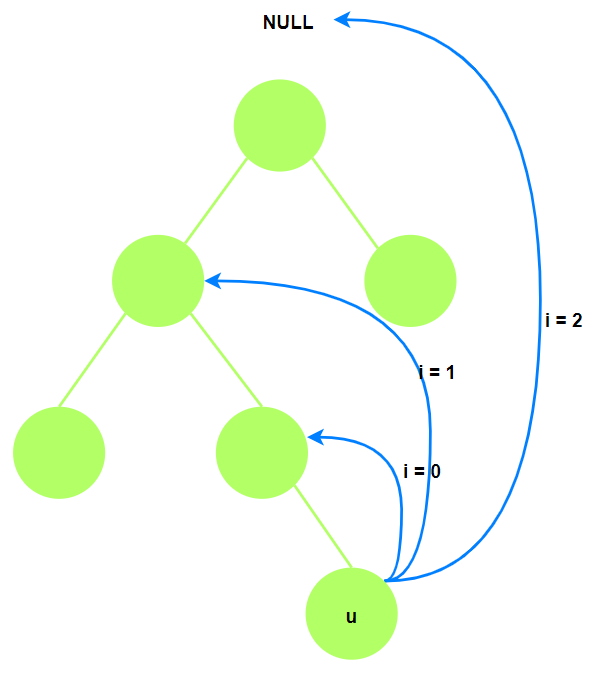
• $fa(u, i)$: 节点$u$向上走$2^i$步的祖先节点. $0\le i\le \lfloor {\lg(|V|)} \rfloor$. 其中$|V|$是树节点个数.

  预处理方式(递推): $i = 0, f(u, 0) = u$的父节点; $i\gt 0$, 两步走, 先走到$2^{i-1}$的祖先节点$v$, 再从$v$向上走$2^{i-1}$步. 即$fa(u, i) = fa( fa(u, i - 1), i - 1)$. 递推顺序: 从祖先到子孙, 所以$f(v, i - 1)$已经在
  之前的递推过程中被预处理过了.

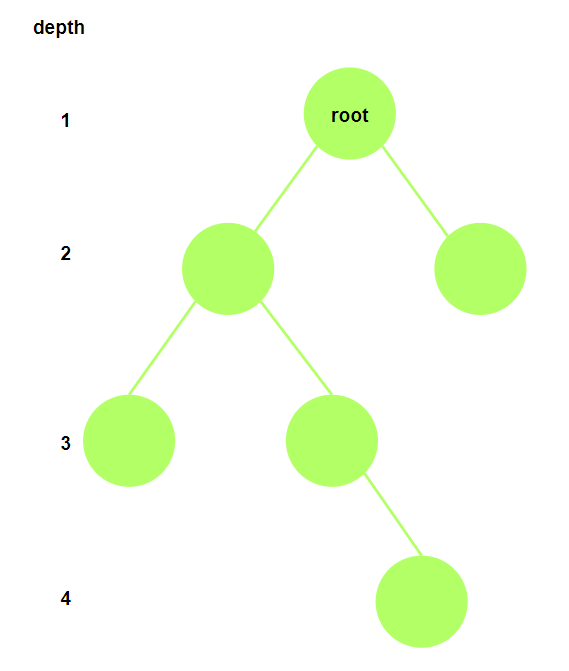
• $depth(u)$: 节点$u$的深度.

  深度: 设根节点的深度为$1$, 节点$u$的直接子节点的深度为$depth(u) + 1$.

求两点$lca$步骤:

1. 分别找到两点处于同义层的父节点. (找层数更深的节点的父节点, 直到其父节点层数与层数低的节点相等).

   寻找过程中使用倍增思想: 对于数字$x$, 按$2^k, …, 16, 8, 4, 2, 1$的顺序判断$x\gt 2^i$是否成立,
   若成立则$x$的二进制表示第$i$位为1, 去掉即可.

2. 若此时没有找到公共祖先, 两点同时向根遍历, 在第一次遇到公共祖先的下一层停止.

具体实现

1. 节点向根遍历过程中可能会跳出根指向NULL, 实现时用0表示NULL. 这样做的好处是在倍增思想中,
   我们不需要额外计算对于$x$, $2^k, …, 8, 4, 2, 1$满足$2^k\le x$的最小的$k$是多少. 此时如果
   计算过程中$2^k\gt x$, 会跳出根节点, 不会计算. 所以具体实现时直接从最大可能的$k$开始判断即可.

2. 求两点$lca$步骤1的倍增思想具体实现 — 这里的$x = depth(a) - depth(b)$, $depth(a)\ge depth(b)$.
   判断是否凑出$x$即判断$depth(a) - depth(b)\ge 0$ --> $depth(a)\ge depth(b)$.
   因为有用0表示NULL的保证, 每次$depth(a)\ge depth(b)$ 成立即可继续向上跳.

3. 实现时为什么在公共祖先的下一层停止 — 如果直接找公共祖先, 可能遇到下述情况:
   
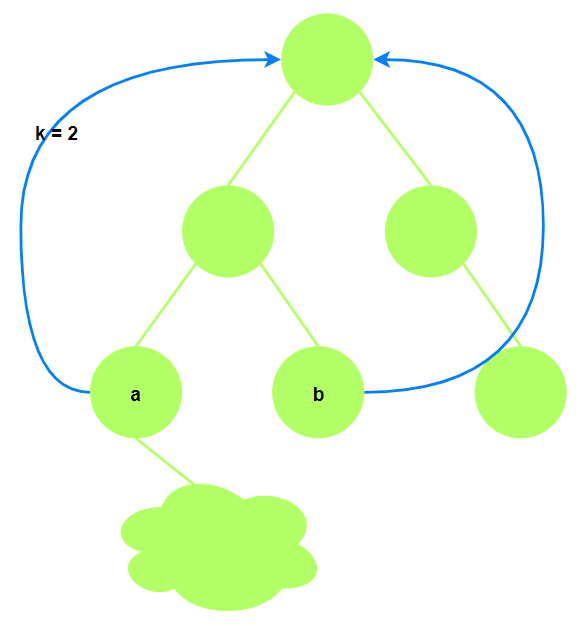
   所以实现时两个节点一直向上跳直到父节点不等 — 跳到离父节点相等(公共祖先)最近的地方, 即公共
   祖先的下一层.

时间复杂度: 倍增法即二进制拼凑思想, 每次查询时间复杂度为$O(\lg(n))$, 初始化时间复杂度$O(n\lg(n))$.

实现代码 $O(n\lg(n) + m\lg(n))$

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 4e4 + 10, M = 2 * N, lgN = 15;

int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], q[N], fa[N][lgN + 1];

void add(int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx ++;
}

void bfs(int root)
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0; //depth[NULL] = 0, 方便步骤1 防止跳出根的判断
    depth[root] = 1;
    int hh = 0, tt = 0;
    q[tt ++] = root;

    while( hh != tt )
    {
        int u = q[hh ++];

        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( depth[v] > depth[u] + 1 ) //未被遍历
            {
                depth[v] = depth[u] + 1;
                q[tt ++] = v;

                fa[v][0] = u; //直接父节点
                for( int k = 1; k <= lgN; k ++ )
                {//递推 如果超出根 fa[v][k] = 0
                    fa[v][k] = fa[ fa[v][k - 1] ][k - 1];   
                }
            }
        }
    }
}

int lca(int a, int b)
{
    if( depth[a] < depth[b] )   swap(a, b); //保证depth[a] >= depth[b]

    for( int k = lgN; k >= 0; k -- )
    {//跳出根会跳过, 所以k可以从最大可能值开始判断
        int pa = fa[a][k]; //如果跳出 depth[NULL] = 0, 不会跳
        if( depth[pa] >= depth[b] )
        {
            a = pa; //倍增思想 能减去则减
        }
    }

    if( a == b )    return a; //其中一个点是两点的公共祖先

   // return 0; 直接返回NULL即可 因为此时两点都不是公共祖先

   for( int k = lgN; k >= 0; k -- )
   {
       int pa = fa[a][k], pb = fa[b][k];
       if( pa != pb )
       {//跳到离公共祖先最近的节点 因为是同一层 所以如果跳出则同时跳出 均为0 会被条件判断pass掉
           a = pa;
           b = pb;
       }
   }
   return fa[a][0]; //lca为两个节点的上一层
}

int main()
{
    cin >> n;
    int root;
    memset(h, -1, sizeof h);
    while( n -- )
    {
        int a, b;
        cin >> a >> b;
        if( b == -1 )   root = a;
        else    add(a, b), add(b, a);
    }

    bfs(root); //预处理

    cin >> m;
    while( m -- )
    {
        int a, b;
        cin >> a >> b;
        int p = lca(a, b);
        if( p == a )    puts("1");
        else if( p == b )   puts("2");
        else    puts("0");
    }

    return 0;
}