题目描述

给你一个整数数组 arr 和一个整数 d。每一步你可以从下标 i 跳到：

• i + x，其中 i + x < arr.length 且 0 < x <= d。
• i - x，其中 i - x >= 0 且 0 < x <= d。

除此以外，你从下标 i 跳到下标 j 需要满足：arr[i] > arr[j] 且 arr[i] > arr[k]，其中下标 k 是所有 i 到 j 之间的数字（更正式的，min(i, j) < k < max(i, j)）。

你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。

请注意，任何时刻你都不能跳到数组的外面。

样例

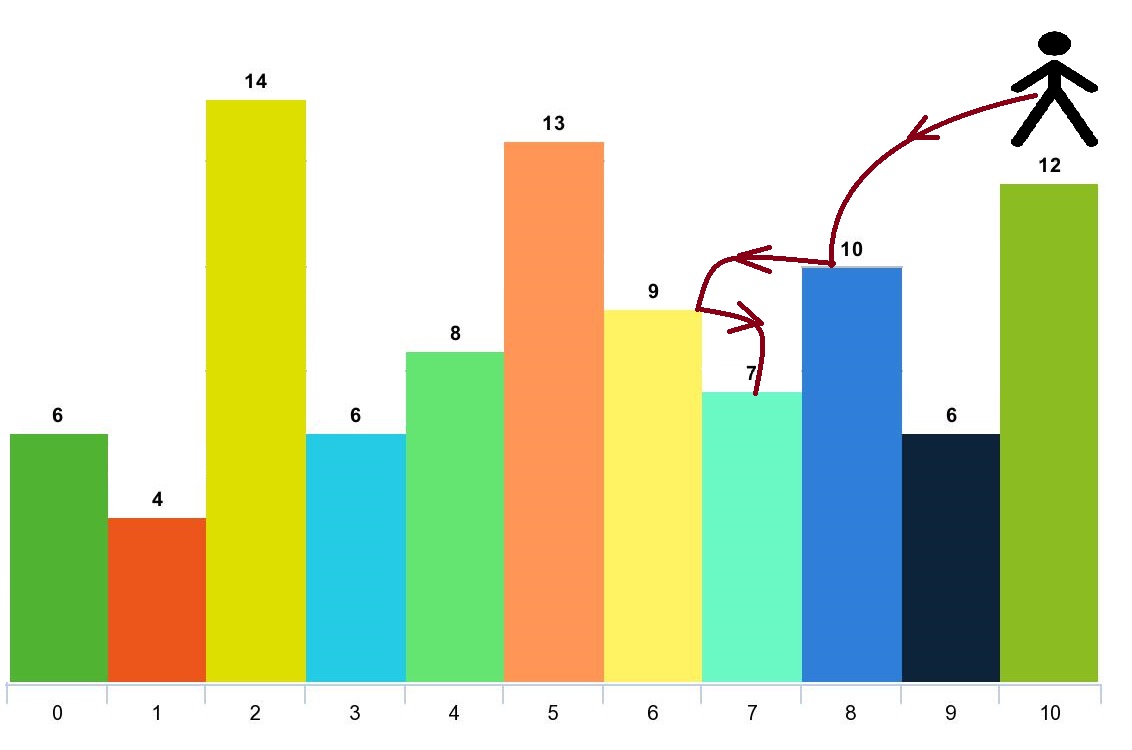
输入：arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
输出：4
解释：你可以从下标 10 出发，然后如上图依次经过 10 --> 8 --> 6 --> 7。
注意，如果你从下标 6 开始，你只能跳到下标 7 处。
你不能跳到下标 5 处因为 13 > 9 。
你也不能跳到下标 4 处，因为下标 5 在下标 4 和 6 之间且 13 > 9。
类似的，你不能从下标 3 处跳到下标 2 或者下标 1 处。

输入：arr = [3,3,3,3,3], d = 3
输出：1
解释：你可以从任意下标处开始且你永远无法跳到任何其他坐标。

输入：arr = [7,6,5,4,3,2,1], d = 1
输出：7
解释：从下标 0 处开始，你可以按照数值从大到小，访问所有的下标。

输入：arr = [7,1,7,1,7,1], d = 2
输出：2

输入：arr = [66], d = 1
输出：1

限制

• 1 <= arr.length <= 1000
• 1 <= arr[i] <= 10^5
• 1 <= d <= arr.length

算法

(记忆化搜索) $O(nd)$

1. 可以发现，如果能从点 i 跳到点 j，则不可能从点 j 跳到点 i，即存在依赖关系，而且每个点的最大步数仅仅依赖于这个点本身。
2. 换句话说，如果之前计算过这个点的答案，就不必再次计算。
3. 所以，我们可以通过记忆化搜索的方式，枚举每个点作为起点，能到达的最短步数。
4. 不方便用循环实现是因为状态的阶段很难划分，而记忆化搜索则可以很方便的找到依赖关系。
5. 设 $f(i)$ 为从点 $i$ 开始的最长步数，转移方程为 $f(i) = \max(f(i), solve(j) + 1)$，其中 $j$ 需要满足题目中的条件。
6. 最终答案就是 $\max(f(i))$。

时间复杂度

• 共有 $n$ 个状态，每个状态需要 $O(d)$ 的时间转移，故时间复杂度为 $O(nd)$。

空间复杂度

• 需要额外 $O(n)$ 的空间记录状态。

C++ 代码

class Solution {
public:
    vector<int> f;
    int n;

    int solve(const vector<int>& arr, int d, int x) {
        if (f[x] > 0)
            return f[x];

        f[x] = 1;
        for (int i = x - 1; i >= max(0, x - d) && arr[x] > arr[i]; i--)
            f[x] = max(f[x], solve(arr, d, i) + 1);

        for (int i = x + 1; i <= min(n - 1, x + d) && arr[x] > arr[i]; i++)
            f[x] = max(f[x], solve(arr, d, i) + 1);

        return f[x];
    }

    int maxJumps(vector<int>& arr, int d) {
        n = arr.size();
        f.resize(n, 0);

        int ans = 0;

        for (int i = 0; i < n; i++)
            ans = max(ans, solve(arr, d, i));

        return ans;
    }
};