区间覆盖

思路分析

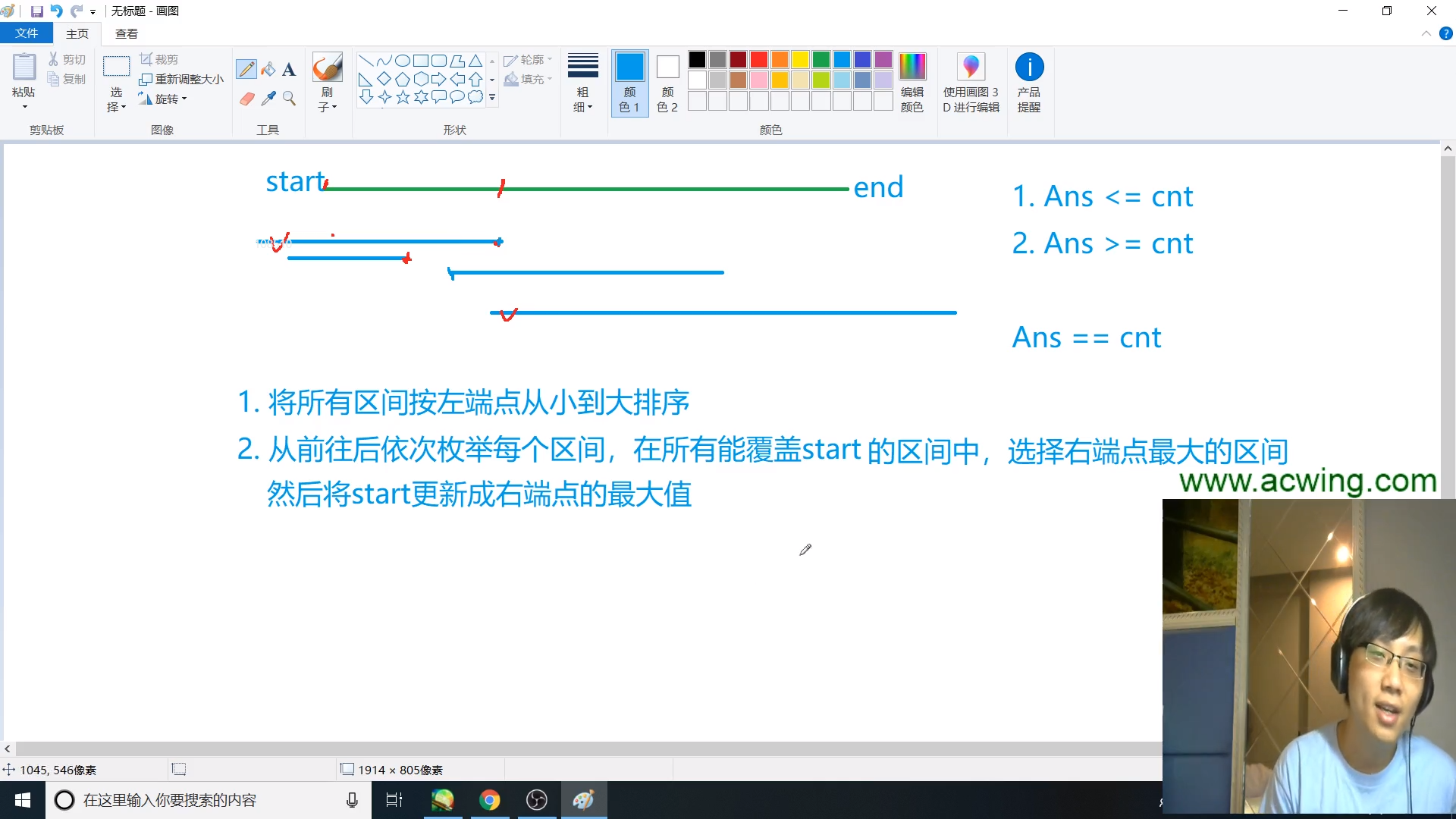
$(1)$ 按左端点升序排列
$(2)$ 每次找可以覆盖目标区间左端点的区间里面右端点最大的。如果当前区间没有能覆盖目标区间左端点的，则无解。如果右端点已经超过目标区间的右端点，则覆盖结束

证明

答案所选择的区间是$ans$，我们用算法得出的区间是$cnt$

从左向右找到第一个不一样的区间，我们可以把答案中的区间替换成$cnt$中对应区间，因为算法求的是能覆盖的区间中右端点最大的，这样不会造成区间数量增大，而且一定可以完美覆盖。依次类推，我们可以将答案求出来的区间全部替换成$cnt$的区间，而不出现区间数量增加

因此两者选出来的区间数量相同

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
struct Range
{
    int l, r;
    bool operator< (const Range &W)const
    {
        return l < W.l;
    }
}range[N];

int main()
{
    int st, ed;
    scanf("%d%d", &st, &ed);
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        range[i] = {l, r};
    }

    sort(range, range + n); // 按左端点升序排列

    int res = 0;
    bool success = false;
    for (int i = 0; i < n; i ++ )
    {
        int j = i, r = -2e9;
        while (j < n && range[j].l <= st) // 找到能覆盖的区间里面，右端点最大的
        {
            r = max(r, range[j].r);
            j ++ ;
        }

        if (r < st) // 如果最大的右端点都覆盖不了目标区间左端点则失败
        {
            res = -1;
            break;
        }

        res ++ ; // 计数区间增加
        if (r >= ed) // 如果已经覆盖了目标区间右端点就结束了
        {
            success = true;
            break;
        }

        st = r;
        i = j - 1; // 因为第j个区间是需要考虑的，后面还有一次递增
    }

    if (!success) res = -1;
    printf("%d\n", res);

    return 0;
}