合并果子

思路分析

思路很简单就是，每次拿出最小的两个果子进行合并，花费体力就是这两个果子重量的和。这是一个哈夫曼树。找最小的果子可以通过堆来实现

证明

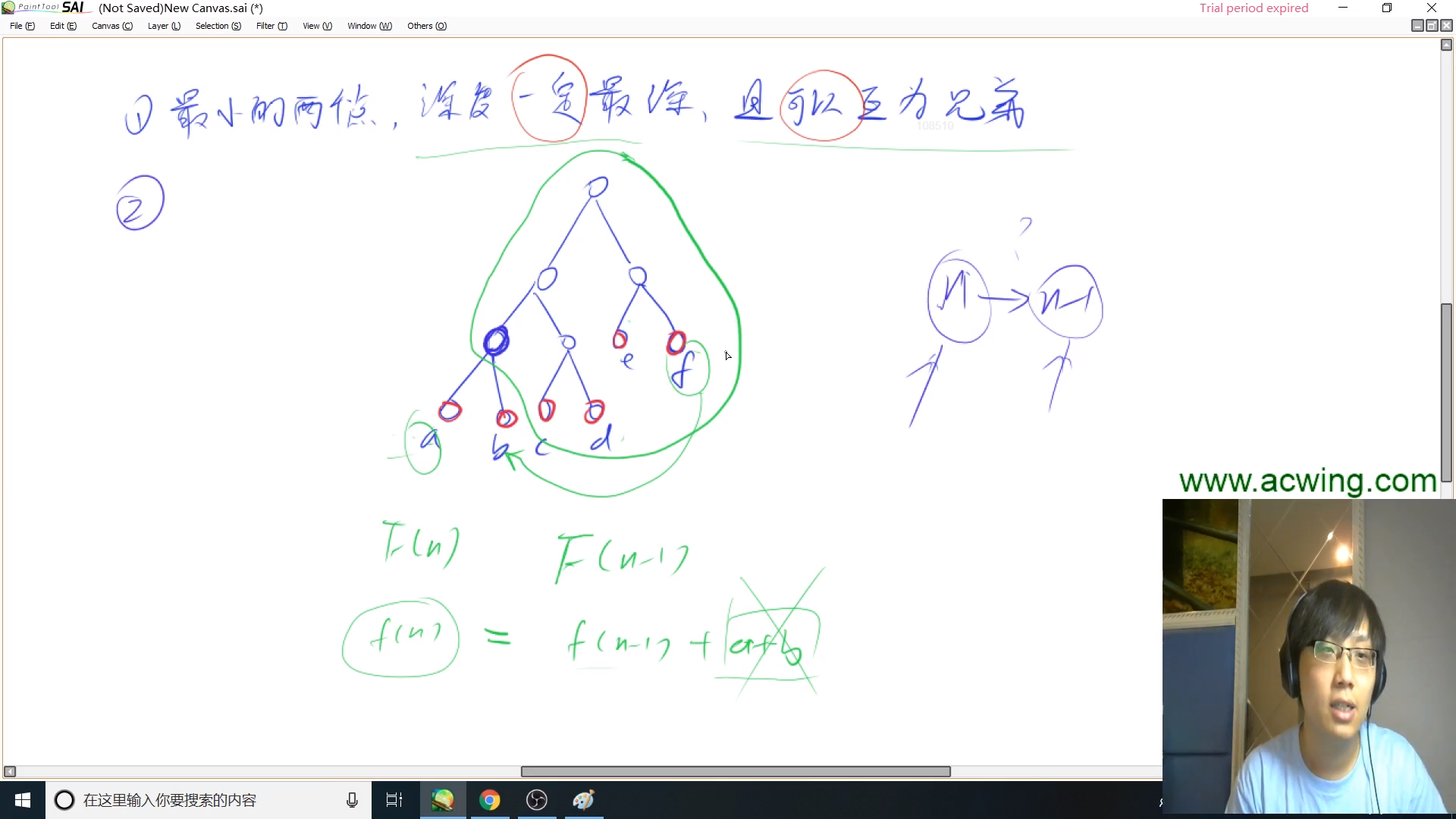
根据题目要求，我们可以建树，叶子结点就是合并的果子。很明显，最轻的果子应该深度最大。这里可以用反证法证明，如果最轻的果子不是深度最深的子节点，那么与深度最深的交换，总能降低消耗的体力。果子只关心位置深度，而与具体位置无关，它可以在最深的一层的任意一个位置。

也就是说对于$n$个果子，先取两个最小的果子合并是最优的。它们会是最深的一层，且为兄弟结点。对于剩下的$(n$ $-$ $1)$，合并它们最少的花费方式也是每次取最小的果子。若f(n)表示合并n个果子的最少体力，则f(n) = a + b + f(n - 1)。(n - 1)的最优解也会导致(n)的最优解。

所以每次取最小的两个果子合并会得到最优解

代码

#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);

    priority_queue<int, vector<int>, greater<int>> heap; // 小根堆
    while (n -- ) // 将数据读入堆
    {
        int x;
        scanf("%d", &x);
        heap.push(x);
    }

    int res = 0;
    while (heap.size() > 1)
    {
        int a = heap.top(); heap.pop();
        int b = heap.top(); heap.pop();
        res += a + b; // 每次合并最小的两个果子
        heap.push(a + b); // 构造剩下(n - 1)个果子的堆
    }

    printf("%d\n", res);
    return 0;
}