滑雪

记忆化搜索

记忆化搜索是对暴搜的一种优化，等价于动态规划。也就是说记忆化搜索是动态规划思想的一种实现方式，是通过搜索来实现的

优点

$(1)$ 记忆化搜索可以避免搜到无用状态，特别是在有状态压缩时
$(2)$ 不需要注意转移顺序（这里的“转移顺序”指正常 dp 中 for 循环的嵌套顺序以及循环变量是递增还是递减）
$(3)$ 边界情况非常好处理，且能有效防止数组访问越界
$(4)$ 有些 dp（如区间 dp) 用记忆化搜索写很简单但正常 dp 很难
$(5)$ 记忆化搜索天生携带搜索天赋，可以使用技能“剪枝”！

缺点

$(1)$ 致命伤：不能滚动数组！
$(2)$ 有些优化比较难加
$(3)$ 由于递归，有时效率较低但不至于 TLE（状压 dp 除外）

思路分析

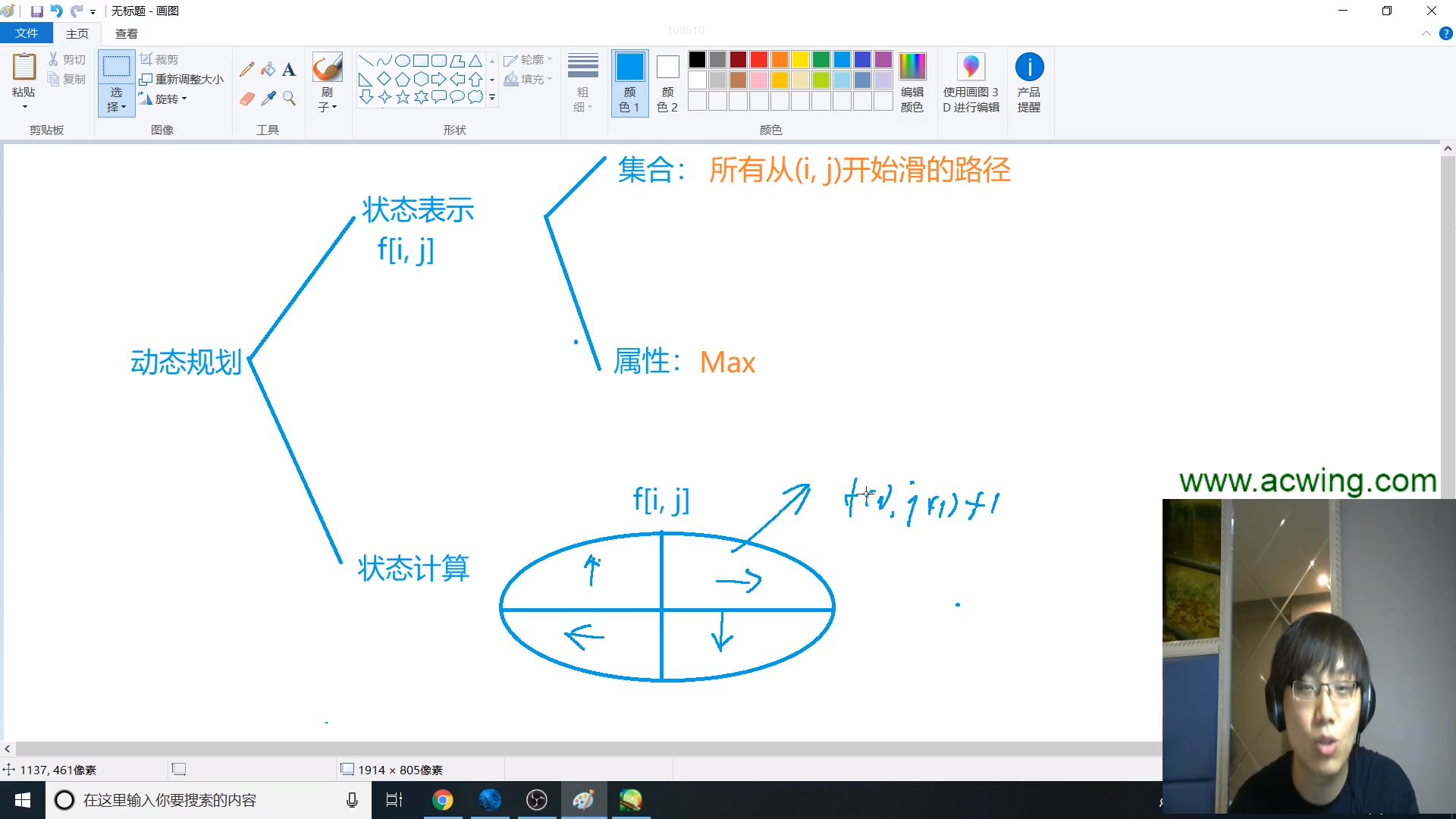
状态表示 $f[i][j]$

集合： 所有从(i, j)开始滑雪的路径
数量： $max$

状态计算

每一个位置都可能向四周下滑，选取可能的状态(当前点比下一个点要高)，并且取最大值

可行性

递归算的时候不能进行死循环，需要是一个拓扑图，而这里面由于高度每次只能向低滑，所以不会出现死循环现象

代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 310;

int n, m;
int g[N][N]; // 建图
int f[N][N]; // dp数组

int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1}; // 偏移量

int dp(int x, int y)
{
    int &v = f[x][y]; // 引用
    if (v != -1) return v; // 算过了就不再算了

    v = 1; // 一个点的路径最少是1，因为包含自己
    for (int i = 0; i < 4; i ++ )
    {
        int a = x + dx[i], b = y + dy[i];
        if (a >= 1 && a <= n && b >= 1 && b <= m && g[x][y] > g[a][b]) // 合法的情况下向四周转移
            v = max(v, dp(a, b) + 1); // 取max
    }

    return v;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &g[i][j]);

    memset(f, -1, sizeof f);
    // -1表示该点还没有走过，初始化起到一个bool数组的作用，判断该点计算过没有

    int res = 0;
    for (int i = 1; i <= n; i ++ ) // 起点可能是每一个点，所以都要尝试
        for (int j = 1; j <= m; j ++ )
            res = max(res, dp(i, j));

    printf("%d\n", res);

    return 0;
}