没有上司的舞会

思路分析

本题中的模型是一种树形，考虑树形Dp

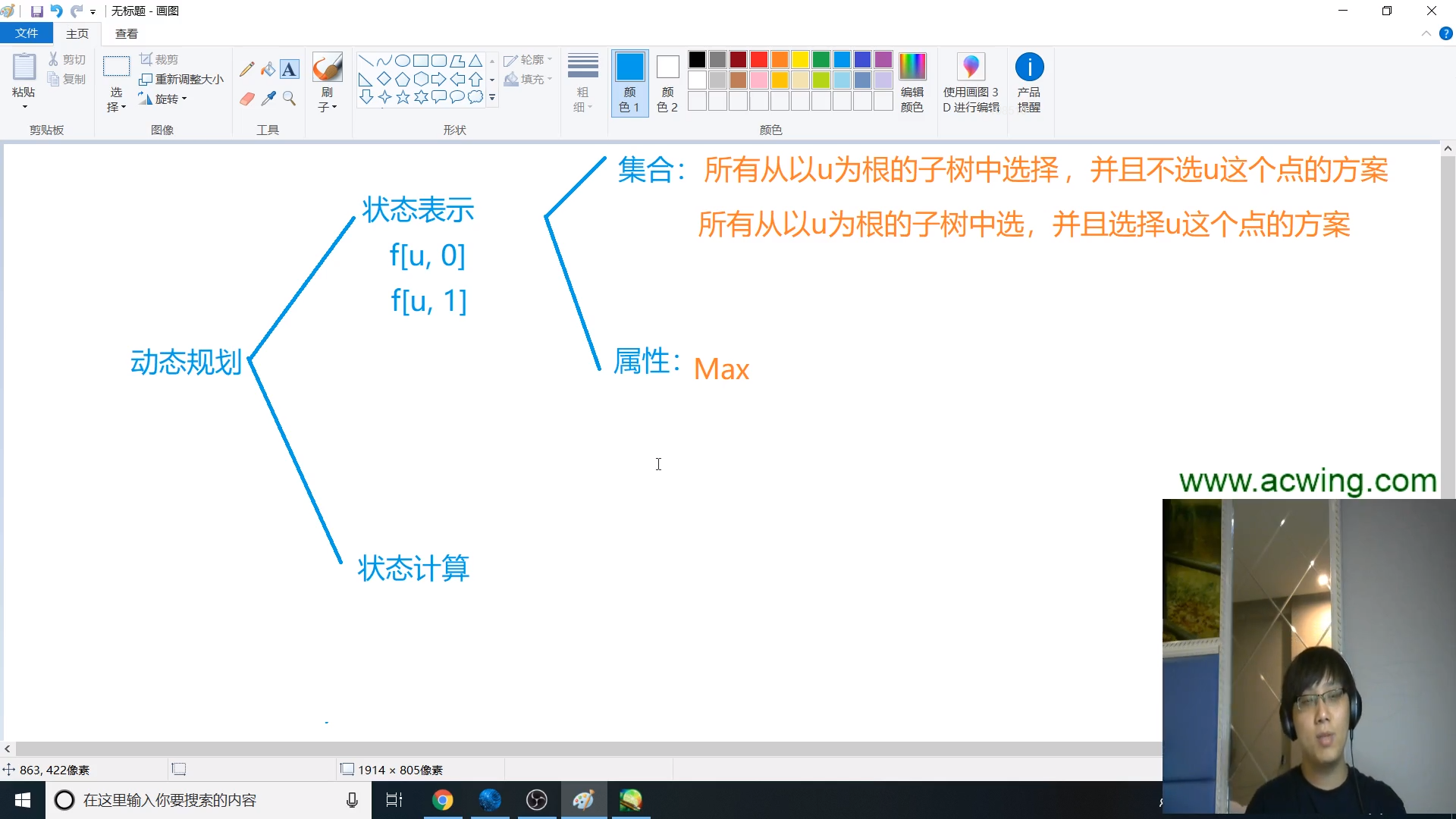
状态表示 $f[i][j]$

集合

$f[u][0]:$ 所有以u为根节点的子树中选择，并且不选u的方案
$f[u][1]:$ 所有以u为根节点的子树中选择，并且选u的方案

属性：$max$

状态计算

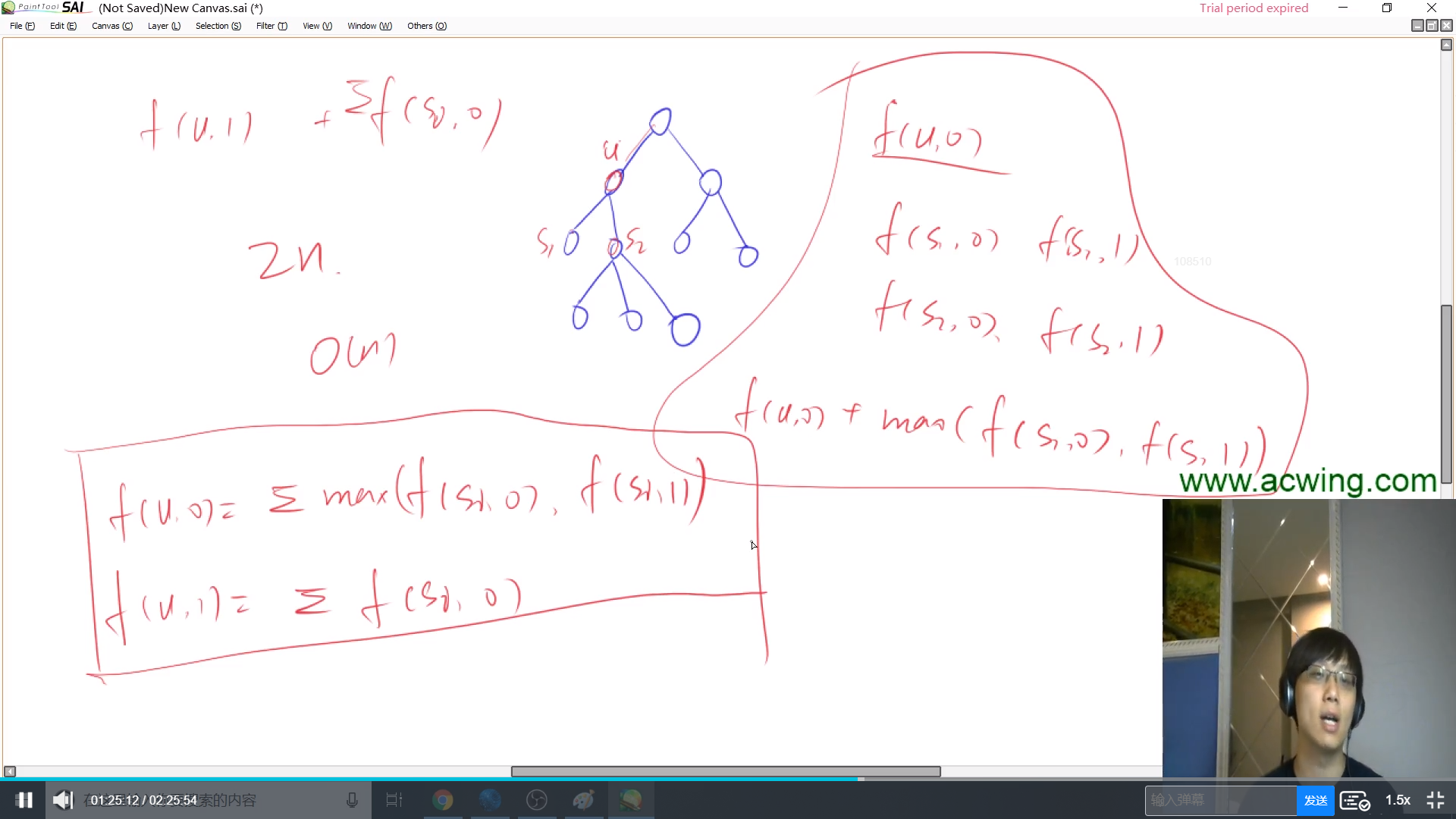
不选根节点时候，那么根节点的子节点的情况可以任选，取最大值

选根节点时，那么一定不能包含子节点，所以子节点的情况只有一种

对于每一个子节点都考虑一下，求和即可

根节点

给数据的时候，并没有直接给出根节点。根据根节点没有父节点这一特性，我们可以开一个$bool$记录结点是否有父节点，最后依此找到根节点

代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 6010;

int n;
int h[N], e[N], ne[N], idx; // 邻接表形式存结点
int happy[N]; // 快乐值
int f[N][2]; // dp 数组
bool has_fa[N]; // 找根节点的数组

void add(int a, int b) // 邻接表添加操作
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u) // dp过程
{
    f[u][1] = happy[u]; // 包含父节点的情况，至少要加上父节点的快乐值

    for (int i = h[u]; ~i; i = ne[i]) // 依此遍历子节点
    {
        int j = e[i]; // 取出子节点序号
        dfs(j); // 递归处理子节点，得出子节点两种情况的快乐值

        f[u][1] += f[j][0]; // 包含父节点只有一种情况
        f[u][0] += max(f[j][0], f[j][1]); // 不含父节点取最大值
    }
}

int main()
{
    scanf("%d", &n);

    for (int i = 1; i <= n; i ++ ) scanf("%d", &happy[i]);

    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b); // a是b的直接上司，所以a是b的父节点
        add(b, a);
        has_fa[a] = true; // 该点有父节点
    }

    int root = 1;
    while (has_fa[root]) root ++ ; // 找根节点

    dfs(root); // dp过程

    printf("%d\n", max(f[root][0], f[root][1])); // 输出最大值

    return 0;
}