最短Hamilton路径

思路分析

我们可以想到最基础的做法就是枚举，这会有n!种情况，很明显，这样会超时

另一个方法就是状态压缩 + dp

考虑角度

若有6个点(0 ~ 5)，到以5号点为重点的最短哈密顿路径等于，到(0 ~ 4)号点的最短距离(中间不经过5号点)加上各自边权在取一次最小值

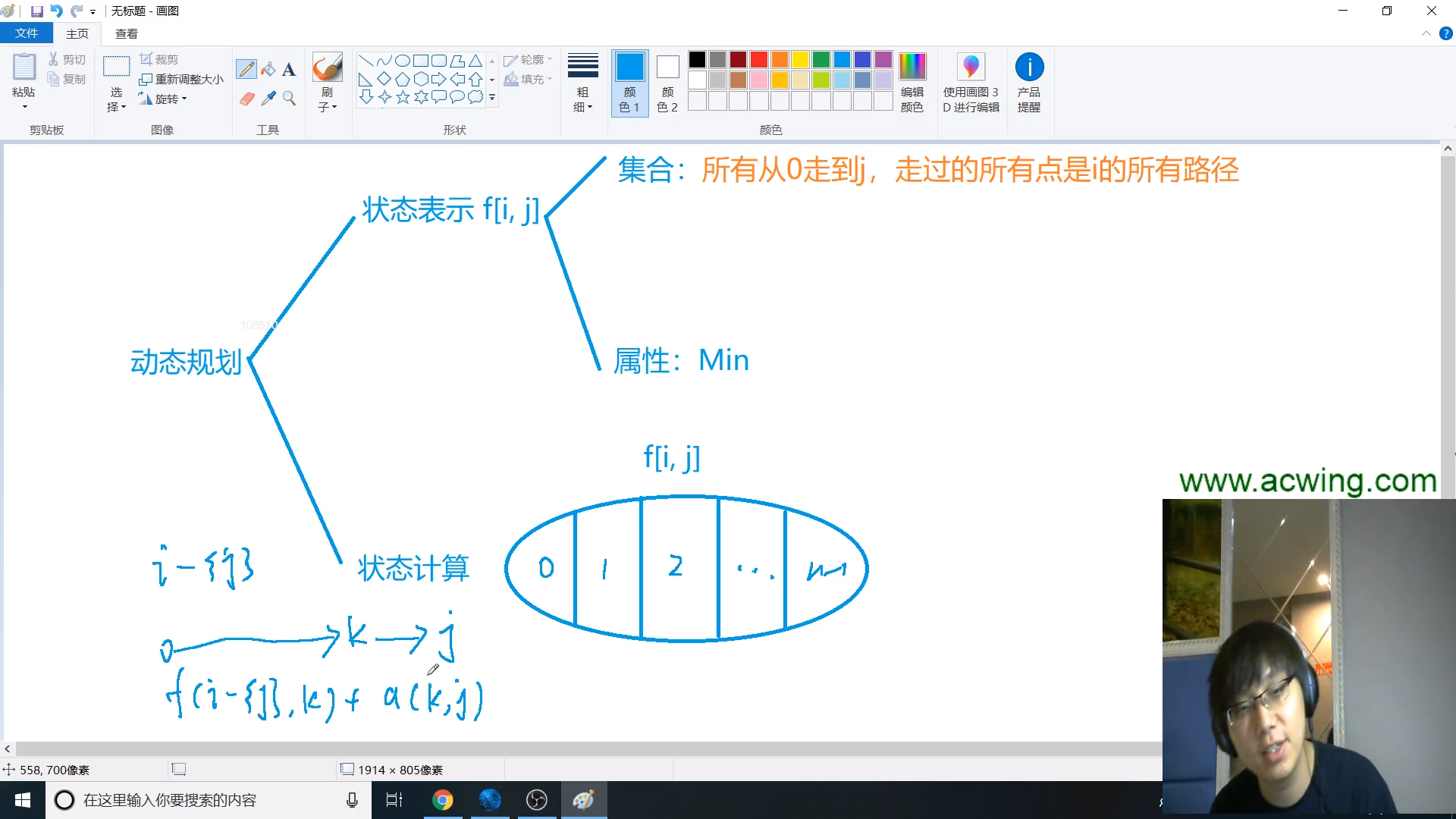
状态表示 $f[i][j]$

$i$表示所有点的经过情况，这里同样运用状态压缩，它的每一位对应一个点的经过与否
$j$表示最后到达的点

集合：经过点数情况是$i$且最终到达的点是$j$的情况
属性：最小值

状态计算

按照中间经过的点分类（这里面的点一定不能包含终点）

f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);

代码

题目要求是从0号点开始，也就是说最后要有一次判断，但是y总没有判断，我也不知道为啥也ac了

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 20, M = 1 << N;

int n;
int w[N][N]; // 边权重
int f[M][N]; // dp数组

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            cin >> w[i][j];

    memset(f, 0x3f, sizeof f); // 因为是求最小值，所以初始化为正无穷
    f[1][0] = 0; // 只经过第0个点到第0个点的距离是0

    for (int i = 0; i < 1 << n; i ++ ) // 枚举中间经过点的所有情况
        for (int j = 0; j < n; j ++ ) // 枚举终点
            if (i >> j & 1) // 如果中间经过j点
                for (int k = 0; k < n; k ++ ) // 枚举倒数第二个点
                    if (i >> k & 1) // 如果经过倒数第二个点
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
                        // 因为i是从小到大枚举的，所以这里f[i - (1 << j][k]一定是之前计算过了的

    cout << f[(1 << n) - 1][n - 1];
    //经过所有的点，终点是(n - 1)号点

    return 0;
}