蒙德里安的梦想

思路分析

我们考虑尽所有的横向摆放方法，剩下的就只有竖着的了。所以总排列方式数量和光摆着竖着、光摆着横着的数量是一样的

状态压缩

一提到表示一列放格有没有使用时候，我们第一反应是用一个bool数组存储，但是这样占用空间比较大

我们可以用一个数字来表示一种情况，数字在电脑中存储是以二进制来存储的，那么我们用这个数字的每一位表示一个位置的状态，这也就是节省了很多的空间

状态表示 $f[i][j]$

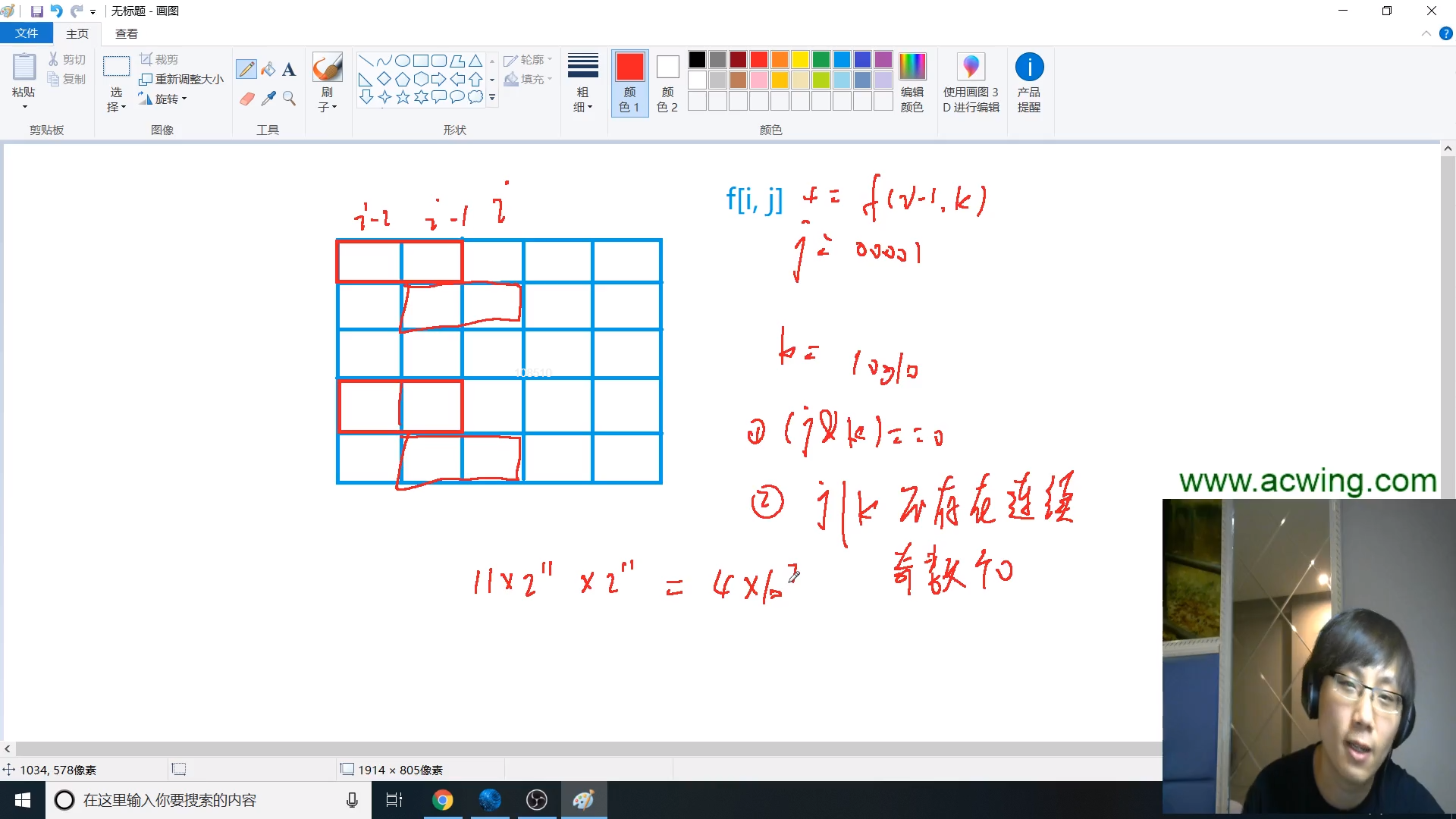
集合：表示在第i行，且从(i - 1)伸出到(i)的卡牌情况是j
属性: 数量

状态计算

合法

上一行状态转移到这一个状态

$(1)$ 首先伸出去的卡牌不能冲突

当前情况与前一行按位与运算，如果有冲突，那么结果不为1.反之，每一位都是0，结果是0

$(2)$ 当前列空余的连续格子都是偶数个

本行格子情况是前一行捅进来和本行伸出去的，所以上一行和本行取或进行判断。奇数偶数判断就用数字和1进行与运算，奇数非0，偶数为0

上面两条是显而易见的，冲突是横着摆不下来。连续格子如果是奇数，那么竖着就摆不下卡牌了

计算

在合法的情况下，k表示上一行伸出的卡牌占用格子情况为k，本行为j
$f[i][j]$ $=$ 所有合法的 $f[i - 1][k]$

代码

朴素写法

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 12, M = 1 << N; // M表示所有排列的可能

int n, m;
long long f[N][M];
bool st[M]; // 当前状态合法与否

int main()
{
    while (cin >> n >> m, n || m)
    {
        for (int i = 0; i < 1 << n; i ++ ) // 排列方式存在连续奇数格子是非法的
        {
            int cnt = 0;
            st[i] = true;
            for (int j = 0; j < n; j ++ )
                if (i >> j & 1)
                {
                    if (cnt & 1) st[i] = false;
                    cnt = 0;
                }
                else cnt ++ ;
            if (cnt & 1) st[i] = false;
        }

        memset(f, 0, sizeof f); // 多次使用，每次重置
        f[0][0] = 1; // 第0行伸出的卡牌一个也没有的情况只有一种，也是初始状态
        for (int i = 1; i <= m; i ++ ) // 枚举列
            for (int j = 0; j < 1 << n; j ++ ) // 枚举每一列可能的伸出情况
                for (int k = 0; k < 1 << n; k ++ ) // 枚举上一列的情况
                    if ((j & k) == 0 && st[j | k]) 
                    // (j & k)是看有没有冲突，st[j | k]是判断格子间隙是否为连续偶数
                        f[i][j] += f[i - 1][k];

        cout << f[m][0] << endl; // 到第m列且没有捅出来的格子
    }
    return 0;
}

去除无效状态的优化写法

上面算法，时间主要是耗费在下面的三重循环了所以我们从优化三重循环入手
我们发现，每一次循环判断本层和上一层的状态是否匹配，上一层能否转移到本层，都是一样的。那么我们可以预处理出来对应的本层情况的上层状态，放到vector里，后面直接用就可以了

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 12, M = 1 << N;

int n, m;
LL f[N][M];
vector<int> state[M]; // 当前状态可以由上一层状态转移过来，记录每一个现态对应的上一层状态
bool st[M];

int main()
{
    while (cin >> n >> m, n || m)
    {
        for (int i = 0; i < 1 << n; i ++ ) // 判格子间没有连续奇数个空格
        {
            int cnt = 0;
            bool is_valid = true;
            for (int j = 0; j < n; j ++ )
                if (i >> j & 1)
                {
                    if (cnt & 1)
                    {
                        is_valid = false;
                        break;
                    }
                    cnt = 0;
                }
                else cnt ++ ;
            if (cnt & 1) is_valid = false;
            st[i] = is_valid;
        }

        for (int i = 0; i < 1 << n; i ++ ) // 预处理
        {
            state[i].clear();
            for (int j = 0; j < 1 << n; j ++ )
                if ((i & j) == 0 && st[i | j])
                    state[i].push_back(j);
        }

        memset(f, 0, sizeof f);
        f[0][0] = 1;
        for (int i = 1; i <= m; i ++ )
            for (int j = 0; j < 1 << n; j ++ )
                for (auto k : state[j]) // 这时候直接用就行，减少重复运算
                    f[i][j] += f[i - 1][k];

        cout << f[m][0] << endl;
    }

    return 0;
}