计数问题

思路分析

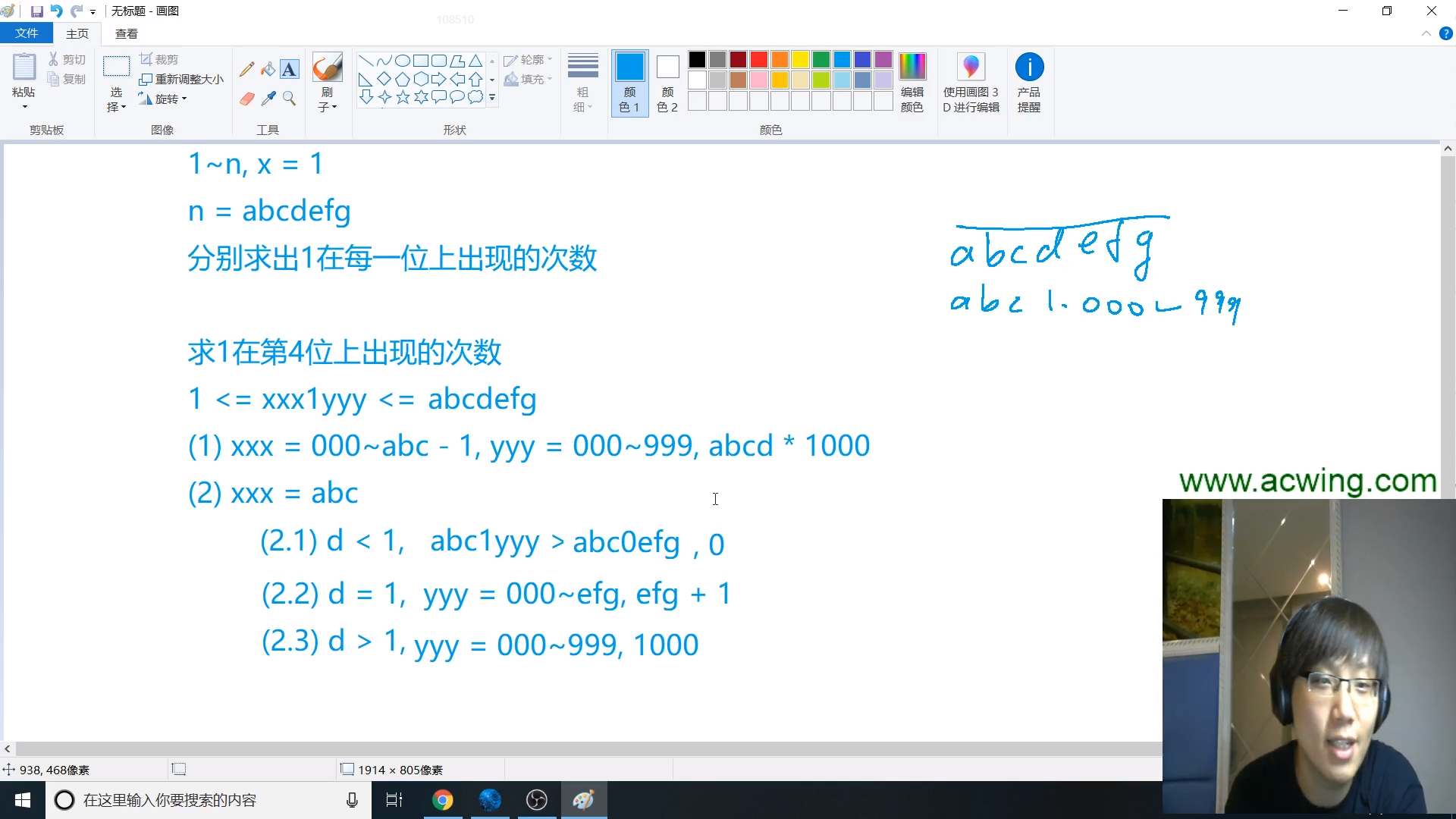
我们需要统计一个区间内0 ~ 9出现的次数，这里运用类似前缀和的思想，实现一个函数功能，统计0 ~ n 区间内各个数字出现的次数。需要求相应区间时候，作差即可

图上整体没问题，就是第一种情况计算0出现的次数时候，由于不能前面数字全是0，所以应该是001 ~ abc
其余部分按图上走就行

看当前位数字前面

如果求的是非0的次数，那么就是前面数字-1，乘上后面的量

如果求的是0，那么前面不能全是0，所以是前面数字-2。同时，0也不能是第一位数字，所以考虑0的时候，得从从左往右的第二位开始考虑

看当前数字的后面

如果当前数字大于所计数的数字，那么就是后面位数都能出现一次

如果相等，那么就出现后面数字 + 1一次，也就是多了全0的情况

如果小于，那么就是0次

代码

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 10;

/*

001~abc-1, 999

abc
    1. num[i] < x, 0
    2. num[i] == x, 0~efg
    3. num[i] > x, 0~999

*/

int get(vector<int> num, int l, int r) // 得到数字一段位数的值
{
    int res = 0;
    for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
    return res;
}

int power10(int x) // 十的乘方运算，pow(10, x)也可以
{
    int res = 1;
    while (x -- ) res *= 10;
    return res;
}

int count(int n, int x) // 计数函数
{
    if (!n) return 0; // 不可能出现的情况，不过也是，如果n是0，计数什么都是0

    vector<int> num; // 将数字扣到vector里面
    while (n)
    {
        num.push_back(n % 10);
        n /= 10;
    }
    n = num.size(); // n是数字位数

    int res = 0; // 存储结果
    for (int i = n - 1 - !x; i >= 0; i -- ) // !x表示如果计数0的时候，就从第二位开始
    {
        if (i < n - 1) // 当位数是从左到右第二位开始，才有左边的数字
        {
            res += get(num, n - 1, i + 1) * power10(i); // 从0000……开始
            if (!x) res -= power10(i); // 如果计数0，则不能全是0，这是非法情况
        }

        if (num[i] == x) res += get(num, i - 1, 0) + 1; 
        // 当前位的数字和计数的数字一样，则是后面数字加上全0，也就是数字 + 1
        else if (num[i] > x) res += power10(i);
        // 大于的时候，后面数字可以任取
    }

    return res;
}

int main()
{
    int a, b;
    while (cin >> a >> b , a)
    {
        if (a > b) swap(a, b); 
        // 题目输入区间，不一定是前面小，后面大。为了方面，我们得前小后大

        for (int i = 0; i <= 9; i ++ )
            cout << count(b, i) - count(a - 1, i) << ' '; 
            // a ~ b 区间内的东西，就是0 ~ b的数量减去0 ~ (a- 1)
        cout << endl;
    }

    return 0;
}