最短编辑距离

思路分析

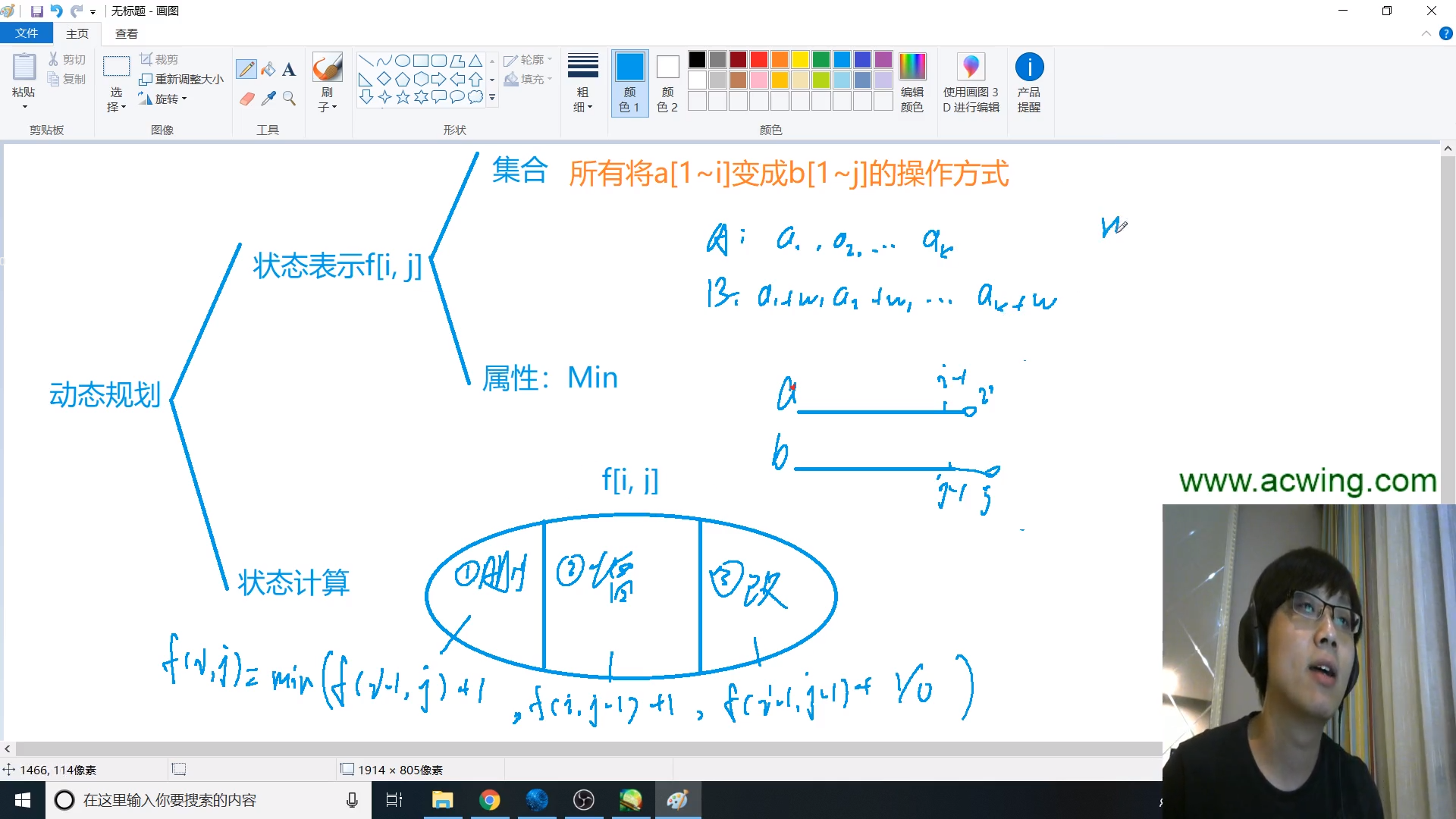
状态表示 f[i][j]

集合：f[i][j]表示的是a串前i个字母变成b串前j个字母的所有方式
属性：数量

状态计算

最后一步总是有三种操作，増删改。我们总是让问题出现的时候，就解决它，所以我们修改的一定是最后一个字母。之前修改的总是会包含在现在，因为我们最后统计方案数量时候，不看修改顺序，只看是怎么修改的

题干是可以删増改任意位置，不过我们在第一时间修改它，所以总会在它是最后一个字母时候就修改它

下面分类也是默认了这个前提

f[i][j] = f[i - 1][j] 删 + f[i][j - 1] 増 + f[i - 1][j - 1] + 1/0 改

a[i] == b[i]时候，就不需要改，反之需要改就加一次操作，最后一步的修改

初始化

第一个字符串前n个字母变成第二个字符串前0个字符时，每次都是删除操作，所以是n

同理，第一个字符串前0个字母变成第二个字符串前n个字符，每次都是添加操作，所以也是n

for (int i = 0; i <= m; i ++ ) f[0][i] = i;
for (int i = 0; i <= n; i ++ ) f[i][0] = i;

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
char a[N], b[N]; // 字符串从1开始存储
int f[N][N]; // dp数组

int main()
{
    scanf("%d%s", &n, a + 1);
    scanf("%d%s", &m, b + 1);

    for (int i = 0; i <= m; i ++ ) f[0][i] = i; // 初始化
    for (int i = 0; i <= n; i ++ ) f[i][0] = i;

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1); // 増和删两种情况一定存在，直接算
            if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]); 
            // 改这一个不一定存在所以分类讨论下
            else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
        }

    printf("%d\n", f[n][m]);

    return 0;
}