算法提高课汇总

题意理解

对于第$i$个区间$[a, b]$, 整数集合中至少有$c$个数字满足$\in [a, b]$.

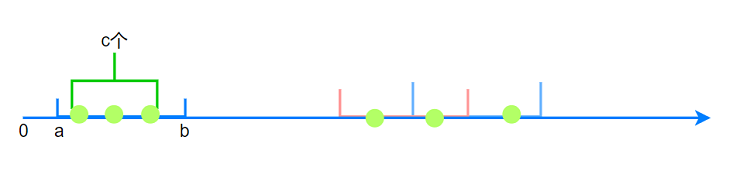
题目求满足上述的整数集合包含整数个数的最小值. 因为$0\le a_i, b_i\le 50000$, 若集合$Z$包含
$0\sim 50000$的所有整数则必定满足条件. 所以问题一定有解.

不等式关系的建立

差分问题的第一步就是从原问题中建立不等式. 整数区间问题, 考虑用前缀和求解. 为方便前缀和计算,
数值从$1$开始, 将上述$a_i, b_i$均加上偏移量$1$.

前缀和:

• $s_i$: 集合从$[1, n]$中选择整数的个数. $1\le i\le 50001$. 下面用$V = 50001$.

• $s_0 = 0$. 符合定义, 且作为求最小值的明确下界.

问题转换为求满足条件的$s_V$最小值. 求最小值用最长路算法求解, 从原题中建立$\ge$的关系.

不等式关系的建立:

• $s_i\ge s_{i-1}, 1\le i\le V$: 前缀和含义的限制.

• $s_i-s_{i-1}\le 1, 1\le i\le V$: --> $s_{i-1}\ge s_i - 1$: 保证整数$i$最多选一次.

• 区间$[a, b]$至少选$c$个: $s_b - s_{a-1}\ge c$ --> $s_b\ge s_{a-1} + c$.

转换为最长路问题:

• 将$s_i$作为顶点, 每个不等式关系作为有向边建图.

• 源点: 需要满足从源点出发能到达所有边. 考虑不等式关系$s_i\ge s_{i-1}, 1\le i\le V$. 相当于有向边:

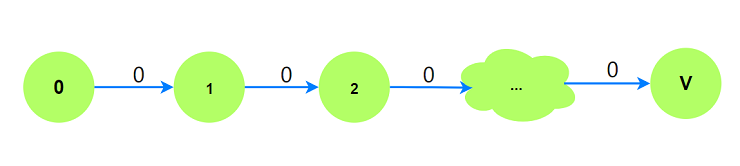
• 从$0$出发可以到达所有顶点, 必然能够到达所有边, 所以以$0$作为源点.

代码实现

$spfa O(nm)$

#include <cstring>
#include <iostream>

using namespace std;

const int V = 50001, N = V + 10, M = 50000 * 3 + 10;

int n;
int h[N], e[M], w[M], ne[M], idx;
int dist[N], q[N]; bool st[N]; 

void add(int u, int v, int c)
{
    e[idx] = v, w[idx] = c, ne[idx] = h[u], h[u] = idx ++;
}

void spfa()
{
    memset(dist, -0x3f, sizeof dist);
    dist[0] = 0;
    int hh = 0, tt = 0;
    q[tt ++] = 0; st[0] = true;

    while( hh != tt )
    {
        int u = q[hh ++];
        if( hh == N )   hh = 0;

        st[u] = false;

        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( dist[v] < dist[u] + w[i] )
            {
                dist[v] = dist[u] + w[i];
                if( !st[v] )
                {
                    st[v] = true;
                    q[tt ++] = v;
                    if( tt == N )   tt = 0;
                }
            }
        }
    }
}

int main()
{
    cin >> n;

    memset(h, -1, sizeof h);
    for( int i = 1; i <= V; i ++ )
    {
        add(i - 1, i, 0); //s(i) >= s(i-1) + 0
        add(i, i - 1, -1); //s(i - 1) >= s(i) - 1
    }

    for( int i = 0; i < n; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        a ++, b ++; // + bias
        add(a - 1, b, c); //s(b) >= s(a-1) + c
    }

    spfa();
    cout << dist[V] << endl; //s(50001) 

    return 0;
}