最长上升子序列 II

思路分析

上升子序列一的算法之所以慢，就在于每次将当前数加入最长子序列时，需要遍历之前的所有数，也就是$O(n)$的

而这一次，我们对这一步骤进行优化，将它优化到$O(n log n)$

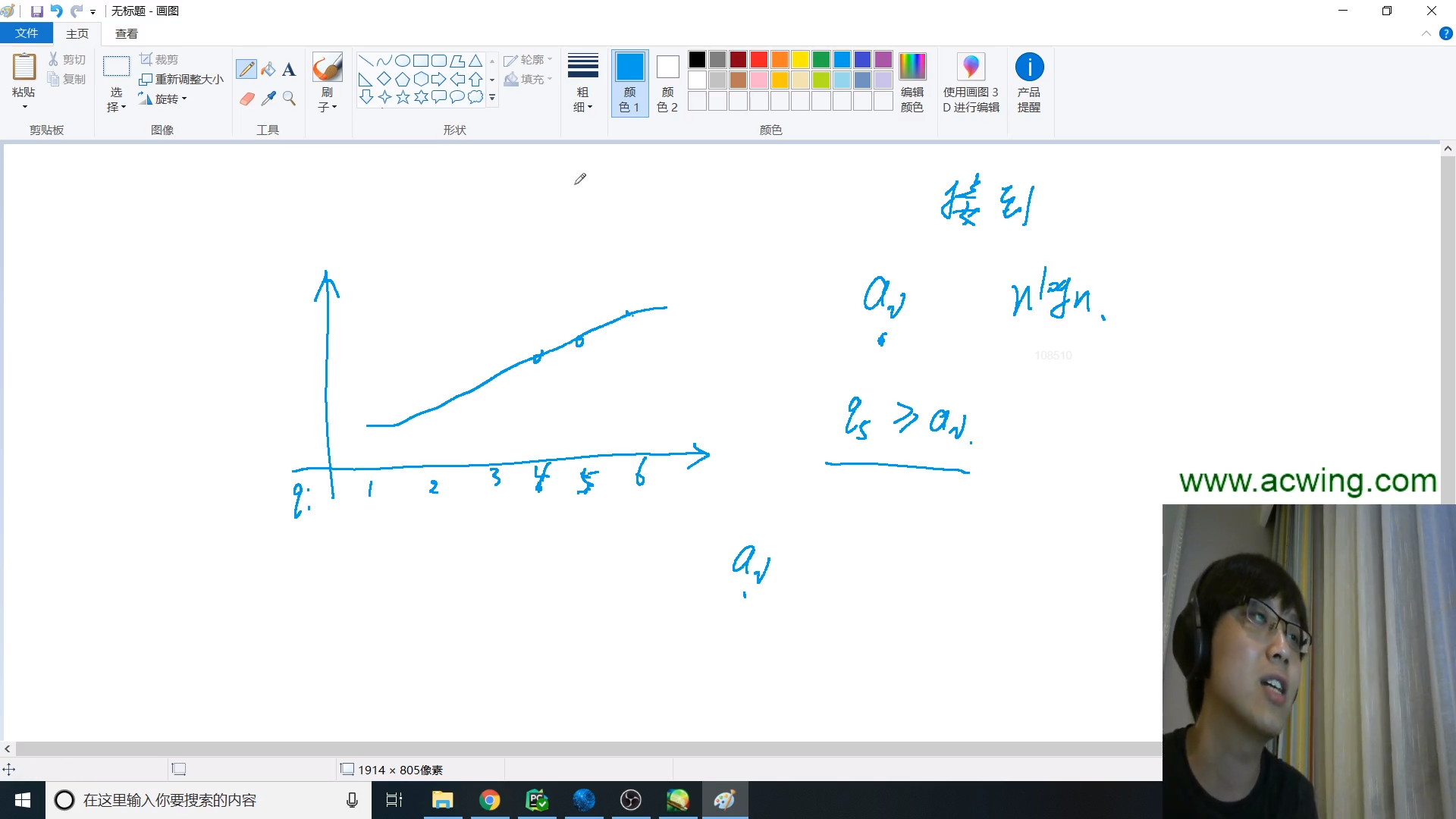
我们开辟一个辅助数组，q[ ], q[i]表示长度为$i$的最长子序列的最后一个数字的最小值

该数组里面元素是单调递增的，也就是子序列长度越大，它的最后一个数字也越大（后面会有证明，我们先用它）

我们每次将一个新的数字插入到子序列时，因为要尽可能的让子序列变长，所以我们要尽可能的向长的子序列后面插入，因为$q$[ ]是单调递增的，所以我们可以二分出来应该添加到哪里，找到数组中比当前数据小的最大值，然后添加到它的后面

添加后，这个最长子序列的长度就会加一，而之前与现在添加后长度相等的子序列最后一个数字比当前处理数据大，所以要修改q[i + 1]

单调性证明

若q[i] >= q[i + 1]

则长度为(i + 1)的子序列里第i个数字 < q[i + 1] < q[i]

也就是说长度为i的最长上升子序列的最后一个数字的最小值不是q[i]，这与定义矛盾了，所以q[i] < q[i + 1]

该数组单调递增

时间复杂度

从前往后考虑每一个数据，单次是$log n$，总共有$n$个数据，所以是$n log n$

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
int a[N]; // 存储数据
int q[N]; // 存储上升子序列的最后一个数的最小值

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]); // 读入数据

    int len = 0; // 当前上升子序列长度最大值
    for (int i = 0; i < n; i ++ ) // 依次处理每一个数据
    {
        int l = 0, r = len; // 二分找到，小于当前数据的最大值
        while (l < r) // 二分过程
        {
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i]) l = mid; // 二分条件
            else r = mid - 1;
        }
        len = max(len, r + 1); 
        // 每次更新完，如果是接到最后的，长度会增加，所以需要考虑上升子序列的最大值是否更新
        q[r + 1] = a[i]; // q[i + 1]也需要更新
    }

    printf("%d\n", len); // 输出上升子序列的最大值

    return 0;
}