算法分析

树形dp + 分组背包

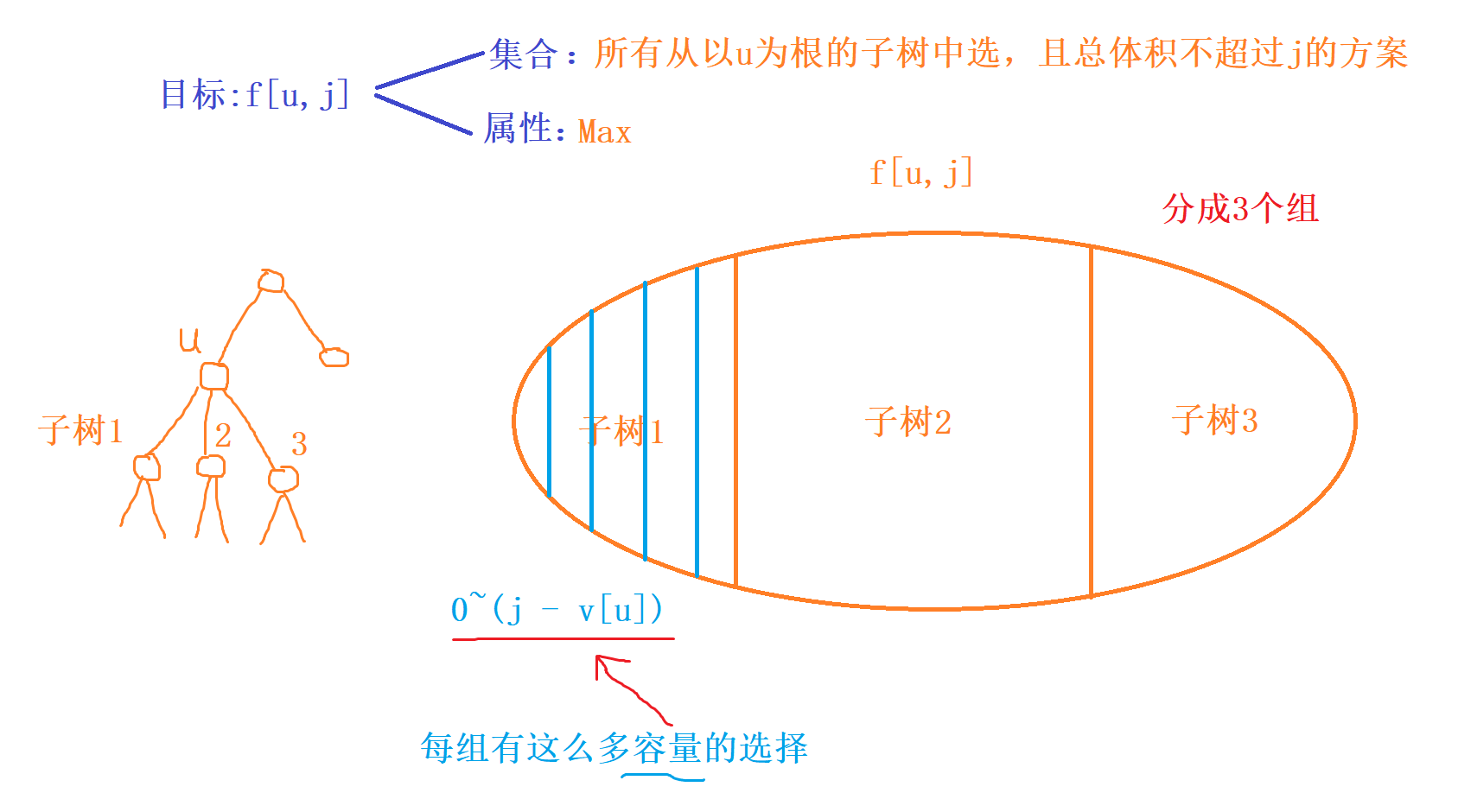
详细代码解释可以参考https://www.acwing.com/solution/acwing/content/5014/

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main{
    static int N = 110;
    static int n;
    static int m;
    static int[] h = new int[N];
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] v = new int[N];
    static int[] w = new int[N];
    static int idx = 0;
    static int[][] f = new int[N][N];
    static void add(int a,int b)
    {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    static void dfs(int u)
    {
        for(int i = h[u];i != -1;i = ne[i]) // 循环物品组
        {
            int son = e[i];
            dfs(son);

            for(int j = m - v[u];j >= 0;j --) // 循环体积
            {
                for(int k = 0;k <= j;k ++) // 循环决策
                {
                    f[u][j] = Math.max(f[u][j], f[u][j - k] + f[son][k]);
                }
            }
        }
        //加上刚刚默认选择的父节点价值
        for(int i = m;i >= v[u];i --)   f[u][i] = f[u][i - v[u]] + w[u];

        for(int i = 0;i < v[u];i ++)    f[u][i] = 0;
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        int root = 0;
        Arrays.fill(h, -1);
        for(int i = 1;i <= n;i ++)
        {
            v[i] = scan.nextInt();
            w[i] = scan.nextInt();
            int p = scan.nextInt();

            if(p == -1) root = i;
            else add(p,i);
        }
        dfs(root);

        System.out.println(f[root][m]);
    }
}