算法提高课汇总

题意理解

对于一个环, 环上边权$t$的数目和点权数$f$相等:

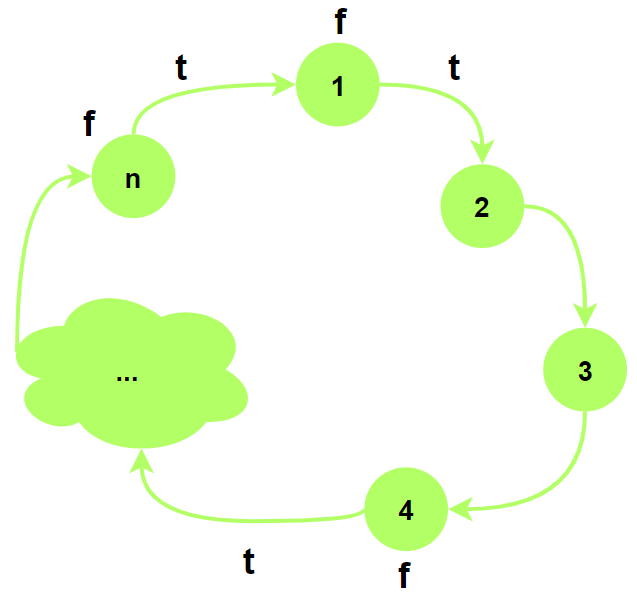
题目要我们找图中环$C$上$\sum f / \sum t$的最大值.

$01$分数规划

在图问题中求形如$\sum f / \sum t$最大值的问题我们称为$01$分数规划 — 经常在图论的
求负环、最小生成树和最短路问题中出现.

$01$分数规划使用二分思路求解: 二分题目要求的点权和除以边权和的最大可能值, 假设某次二分的值为$mid$.

判断图中是否存在环$C$, 使得$\sum f / \sum t\gt mid$:

$\;\;\;\;\sum f / \sum t\gt mid$ <--> $\sum f \gt mid\times \sum t$. <--> $\sum f - mid\times \sum t\gt 0$

为方便计算, 我们将点权放入边权中: 可以将$f(u)$放入边$u\rightarrow v$中(即$u$的出边, 入边也可).

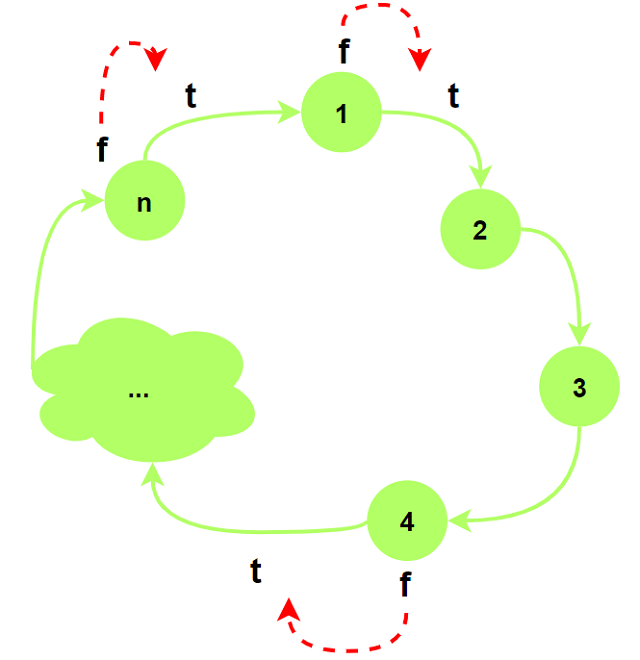
这里的加入只是便于理解, 加入不是指将点权和边权相加, 而可以认为是给这条边加上一个独立的属性值.
可以这么做是因为这对求环的比值没有数值影响.

公式转换为: $\sum (f_i - mid\times t_i)\gt 0$.

也就是我们将所有边的边权从$t_i\rightarrow f_i - mid\times t_i$, 问题转化为判断图中是否存在正环.

求正环问题可以将所有边权取负, 再判断是否存在负环; 或者可以求最长路的边数:

• 核心是求更新次数: 如果存在正环, 则每经过一次正环最长路数值都会增大, 所以算法会经过无数次(超过$n$次).

$01$规划思路: 二分得到一个常数 --> 重新定义边权 --> 图论问题.

代码实现

• 浮点数的二分中, 经验上如果保留到$n$位小数, 我们的精度设为$n + 2$位.

#include <cstring>
#include <iostream>

using namespace std;

const int N = 1010, M = 5010;

int n, m;
int wf[N]; 
int h[N], e[M], wt[M], ne[M], idx;
double dist[N]; int q[N]; bool st[N]; //spfa
int cnt[N];

void add(int u, int v, int c)
{
    e[idx] = v, wt[idx] = c, ne[idx] = h[u], h[u] = idx ++;
}

bool check(double mid)
{
    memset(st, 0, sizeof st); //因为spfa不是完整执行后退出 而可能在运行到中间退出
    memset(cnt, 0, sizeof cnt);
    int hh = 0, tt = 0;
    for( int i = 1; i <= n; i ++ )
    {
        q[tt ++] = i;
        st[i] = true;
    }

    while( hh != tt )
    {
        int u = q[hh ++];
        if( hh == N )   hh = 0;

        st[u] = false;

        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            double w = wf[u] - mid * wt[i];
            if( dist[v] < dist[u] + w )//求最长路
            {
                dist[v] = dist[u] + w;
                cnt[v] = cnt[u] + 1;

                if( cnt[v] == n )   return true;

                if( !st[v] )
                {
                    st[v] = true;
                    q[tt ++] = v;
                    if( tt == N )   tt = 0;
                }
            }
        }
    }
    return false;
}

int main()
{
    cin >> n >> m;

    for( int i = 1; i <= n; i ++ )  cin >> wf[i];
    memset(h, -1, sizeof h);
    while( m -- )
    {
        int u, v, c;
        cin >> u >> v >> c;
        add(u, v, c);
    }

    double l = 0, r = 1000;
    while( r - l > 1e-4 )
    {
        double mid = (l + r) / 2;
        if( check(mid) )    l = mid;
        else    r = mid;
    }
    printf("%.2lf\n", l);

    return 0;
}