算法提高课汇总

$spfa$ 求负环

负环

图$G$中存在回路$C$, $C$中所有边的边权和为负数.

为何要单独考虑负环?

• 在最短路问题中, 如果图中起点$s$到某个顶点$u$的过程中经过负环, 因为每经过一次负环最短路径值都会减少,
  所以算法会陷入死循环, 最后$dist[u]\rightarrow -\infty$.

$spfa$求负环

方法$1$

• 统计每个点入队次数, 如果某个点入队$n$次, 说明存在负环.

• 正确性证明: $spfa$算法是$bellman\;ford$算法的改进, 每次顶点$u$入队相当于$bellman\;ford$
  算法中$dist[u]$被更新, 而更新的次数对应最短路径的长度. 顶点$u$更新$n$次说明从起点到$u$
  存在一条边数为$n$的路径, 路径经过$n + 1$个顶点. 根据抽屉原理, 路径中至少有一个顶点
  出现两次, 也就是路径中存在环路. 而算法保证只有距离减少才会更新, 所以环路权值之和为负数.

方法$2$

• 统计从起点到任意顶点最短路经过的边数, 若某点对应边数$cnt\ge n$, 则也说明负环.

• 正确性证明: 直观理解, 可以用上论述过程说明存在负环.

一般使用方法$2$, 考虑下图:

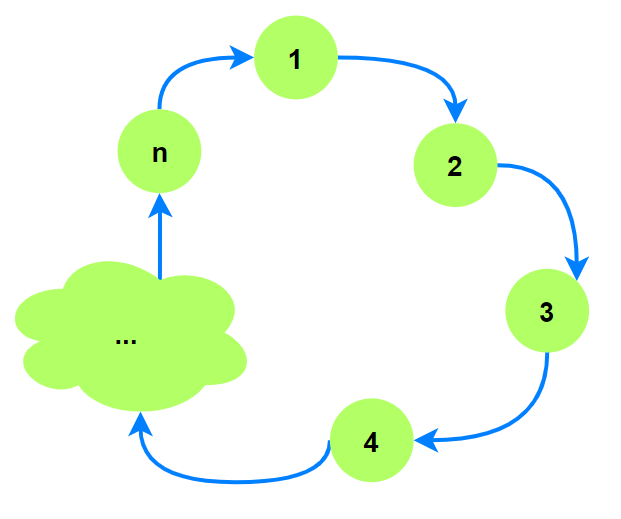
假设起点为$1$:

• 对于方法$1$, 从$1$沿着环更新走到$n$, 所有顶点入队一次. 那么只有沿着环走$n - 1 + 1$次(回到$1$)
  才能判断图中存在负环. 时间复杂度$O(n^2)$.

• 对于方法$2$, 从$1$沿着环更新走到$n$, 此时从起点到$n$经过的路径数为$n - 1$, 当再次回到$1$时我们
  就可以判断图中存在负环. 时间复杂度$O(n)$.

负环与起点不连通

为防止起点与负环不连通导致我们不能准确判断图$G$是否存在负环的情况, 我们进行如下操作:

• 将所有顶点加入队列.

• 将所有顶点最短距离$dist[u]$初始化为$0$.

对于我们可以将所有顶点加入队列的理解:

• 建立虚拟源点$s$, 从$s$向所有顶点连一条权值为$0$的边. 新图与原图的最短路径相同, 且任意负环都与
  源点$s$联通. 将$s$加入队列, 再依次将所有顶点入队等价于直接将所有顶点入队.

为何可以将距离初始化为$0$:

• 若图$G$中存在负环, 则从起点到负环上的点经过$spfa$算法不加停止的计算后, 最终环上顶点的距离
  $dist[u] = -\infty$. 而只要初始值为一个有限值, 且边权为有限值, 我们就需要经过无穷次负环
  才能将距离更新为$-\infty$, 超过了$n$次, 所以不论初值是多少, 算法都能判断出图中存在负环.
  一种简单理解: 找负环的关键是计算距离被更新的次数, 而不是距离的数值. 只要存在负环某些点的
  最短路就一定会被更新.

小技巧

虽然$spfa$算法最好的时间复杂度为$O(m)$, 但经验上来看在求负环时$spfa$时间复杂度常接近$O(nm)$.
这在某些问题中很可能会超时. 一个取巧的方法是当我们发现$spfa$的效率比较接近$O(nm)$时, 就
可以认为图中存在负环. 这种方式大概率可以得到正确结果.

例如当所有点的入队次数大于$2n$时, 就可以假定图中存在负环.

代码实现

本题为朴素的求负环问题.

$spfa\;O(nm)$

#include <cstring>
#include <iostream>

using namespace std;

const int N = 510, M = 2500 * 2 + 200 + 10;

int n, m1, m2;
int h[N], e[M], w[M], ne[M], idx;
int dist[N], q[N]; bool st[N]; //spfa
int cnt[N]; //cnt[u]: 某点到u最短路边数

void add(int u, int v, int c)
{
    e[idx] = v, w[idx] = c, ne[idx] = h[u], h[u] = idx ++;
}

bool spfa()
{
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    int hh = 0, tt = 0;
    for( int i = 1; i <= n; i ++ )
    {
        q[tt ++] = i;
        st[i] = true;
    }

    while( hh != tt )
    {
        int u = q[hh ++];
        if( hh == N )   hh = 0;

        st[u] = false;

        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( dist[v] > dist[u] + w[i] )
            {
                dist[v] = dist[u] + w[i];
                cnt[v] = cnt[u] + 1;

                if( cnt[v] == n )   return true;

                if( !st[v] )
                {
                    st[v] = true;
                    q[tt ++] = v;
                    if( tt == N )   tt = 0;
                }
            }
        }
    }
    return false;
}

int main()
{
    int T;
    cin >> T;
    while ( T -- )
    {
        cin >> n >> m1 >> m2;

        memset(h, -1, sizeof h);
        idx = 0;

        while ( m1 -- )
        {
            int u, v, c;
            cin >> u >> v >> c;
            add(u, v, c), add(v, u, c);
        }
        while ( m2 -- )
        {
            int u, v, c;
            cin >> u >> v >> c;
            add(u, v, -c);
        }

        if( spfa() )    puts("YES");
        else    puts("NO");
    }
    return 0;
}