算法提高课汇总

算法思路

将一颗树扩充为完全图, 考虑一种增加边的顺序:

• 按照原树边权从小到达的顺序, 将边两个端点所属的两个连通块构建为一个子完全图.

假设当前最小边权边为$e$:

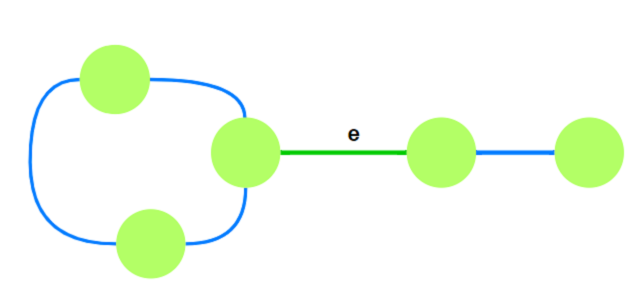
则构建后子完全图为:

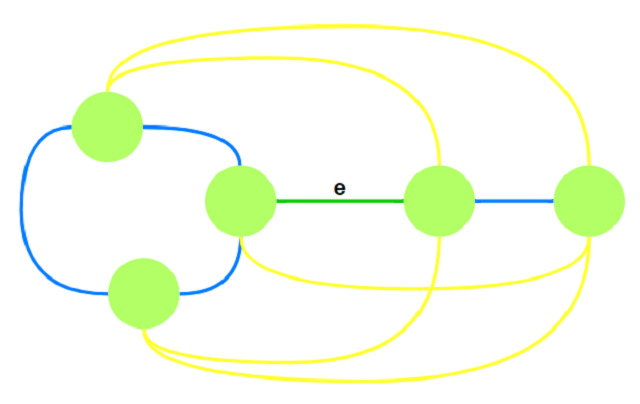
再考虑新加的某条边的边权, 假设新加边权为$w’$, $e$的边权为$w$:

• $w’\lt w$: 假设原树为最终完全图的最小生成树$T$, 则我们增加边的顺序是按照$Kruskal$算法顺序遍历的.
  我们知道$e\in T$, 若此时加入新加入的$w’$构成回路$C$. 可以证明去掉$w$保留$w’$会得到一个更优的生成树,
  与题意最小生成树矛盾.

• $w’ = w$, 按照上相同思路, 可以证明去掉$w$保留$w’$会得到权值和相同的生成树, 与题意唯一矛盾.

• $w’\gt w$. 我们只剩下这个选择. 则新加入边的可能最小权重为$w’ = w + 1$.

如果按边权递增顺序每次增加边权都是对应最小边权$w + 1$, 可以得到可能答案的最小值. 即$ans\ge t$.
$t$指的是所有新加入边均取可能最小值的权重之和. 那么$ans$能否取到其理论最小值$t$呢?

• 假设可以, 即每次加入的边权均为对应的最小值满足题意. 反证法: 如果用这种方式最终的最小生成树不唯一, 也就是
  存在另一颗树$T’, W(T’) = W(T)$. 因为算法加边方式保证在$Kruskal$求最小生成树过程中, 原树的边权均
  是我们可选的最小值, 所以如果$T’$中第$k$次选择的边不在$T$内, 其边权一定大于$T$第$k$大的边, 与假设$W(T’) = W(T)$矛盾.

也就是说上述加边方式保证了在$Kruskal$算法求最小生成树的过程中, 原树的边权均是唯一可选最小边.

代码实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 6010;

int n;
int p[N], cize[N]; //cize[u]: 若u是并查集的根, 则cize[u]表示其集合大小.(只保证对根正确即可)
struct Edge
{
    int u, v, w;
    bool operator< (const Edge &edge) const
    {
        return w < edge.w;
    }
}e[N];

void init(int n)
{
    for( int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        cize[i] = 1;
    }
}

int find(int x)
{
    return x == p[x] ? x : p[x] = find(p[x]);
}

int main()
{
    int T;
    cin >> T;
    while ( T -- )
    {
        cin >> n;
        for( int i = 0; i < n - 1; i ++ )
        {
            int u, v, w;
            cin >> u >> v >> w;
            e[i] = {u, v, w};
        }

        init(n);
        sort(e, e + n - 1);

        int res = 0;
        for( int i = 0; i < n - 1; i ++ )
        {
            int u = find(e[i].u), v = find(e[i].v), w = e[i].w;
            if( u != v )
            {//建立完全图
                res += (cize[u] * cize[v] - 1) * (w + 1); //边数 * 边权
                p[u] = v; //v作为新连通块的根
                cize[v] += cize[u];
            }
        }
        cout << res << endl;
    }
    return 0;
}