算法提高课汇总

模型抽象

• 建立联系后每两个村庄都能直接或间接通讯: 构建连通图.

• $k$个卫星: 可以让$k$个顶点免费连接通讯.

• 型号相同的$d$: 连接剩余顶点的边中边权的最大值.

算法思路$1$

考虑我们确定了型号$d$, 则所有距离$dist\le d$的村庄可以建立联系, 在图中建立了若干连通块.

可以构建联系的距离最大值$d$与联通图的数量是成反比的. 考虑若$d = 0$, 则图中无边, 共有$n$个
连通块; 而当$d$大于等于图中所有边权最大值时, 所有顶点自然联通, 共有$1$个连通块.

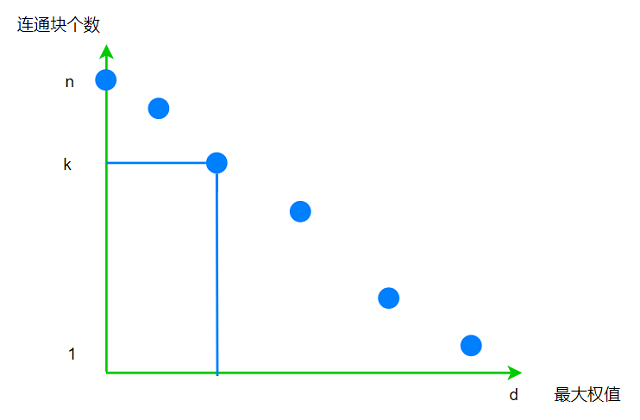
而题目的要求即是: 找到满足连通块个数不超过$k$个的最小的$d$.

考虑$Kruskal$的计算过程:

• 按照边权递增的顺序, 当把两个不联通的顶点联通时, 相当于在图中减少了一个连通块. 在连通块
  恰好减少到$k$时, 对应的边权因为有递增的保证, 所以是满足条件的最小边权.

代码实现

#include <cmath>
#include <iostream>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int, int> pii;

const int N = 510, M = N * N / 2;

int n, m, k;
int p[N]; 
pii points[N];
struct Edge
{
    int u, v;
    double w;
    bool operator< (const Edge &edge) const
    {
        return w < edge.w;
    }
}e[M];

double get_dist(const pii &p1, const pii &p2)
{
    double dx = p1.x - p2.x;
    double dy = p1.y - p2.y;
    return sqrt(dx * dx + dy * dy);
}

int find(int x)
{
    return x == p[x] ? x : p[x] = find(p[x]);
}

double kruskal()
{
    for( int i = 1; i <= n; i ++ )  p[i] = i; //初始化并查集
    sort(e, e + m);
    int cnt = n; //初始连通块个数
    double res = 0; //初始边权 
    for( int i = 0; i < m; i ++ )
    {

        if( cnt <= k )  break; //找到最终解 这样写的好处是不用考虑k = 0的情况

        int u = find(e[i].u), v = find(e[i].v); 
        double w = e[i].w;
        if( u != v )
        {
            p[u] = v;
            cnt --;
            res = w;
        }
    }
    return res;
}

int main()
{
    cin >> n >> k;
    for( int i = 1; i <= n; i ++ )
        cin >> points[i].x >> points[i].y;
    for( int i = 1; i <= n; i ++ )
        for( int j = i + 1; j <= n; j ++ )
        {
            e[m ++] = {i, j, get_dist(points[i], points[j])};
        }

    printf("%.2lf\n", kruskal());

    return 0;
}

算法思路$2$

考虑从原图中建立一颗最小生成树$T$后, 我们可以让$k$个顶点免费相连, 也就是让$k - 1$条边
($k = 0$时特殊考虑)免费. 则最大的边权为$T$中权值第$n - 1 - (k - 1)$大的边权.(共有$n - 1$条边)

仍考虑$Kruskal$算法求解:

• 算法保证边权按递增顺序被选择, 所以此时第$n - 1 - (k - 1)$大的边权也是所有最小生成树中满足条件
  的最小边权.

代码实现

#include <cmath>
#include <iostream>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int, int> pii;

const int N = 510, M = N * N / 2;

int n, m, k;
int p[N]; 
pii points[N];
struct Edge
{
    int u, v;
    double w;
    bool operator< (const Edge &edge) const
    {
        return w < edge.w;
    }
}e[M];

double get_dist(const pii &p1, const pii &p2)
{
    double dx = p1.x - p2.x;
    double dy = p1.y - p2.y;
    return sqrt(dx * dx + dy * dy);
}

int find(int x)
{
    return x == p[x] ? x : p[x] = find(p[x]);
}

double kruskal()
{
    for( int i = 1; i <= n; i ++ )  p[i] = i; //初始化并查集
    sort(e, e + m);

    double res = 0; //记录答案
    int cnt, count = 0; //答案是Kruskal选择边中第cnt大的边
    if( k == 0 )    cnt = n - 1; //最后一个
    else    cnt = n - 1 - (k - 1);

    for( int i = 0; i < m; i ++ )
    {
        int u = find(e[i].u), v = find(e[i].v); 
        double w = e[i].w;
        if( u != v )
        {
            p[u] = v;
            count ++;
            if( count == cnt )  //找到答案
                res = w;
        }
    }
    return res;
}

int main()
{
    cin >> n >> k;
    for( int i = 1; i <= n; i ++ )
        cin >> points[i].x >> points[i].y;
    for( int i = 1; i <= n; i ++ )
        for( int j = i + 1; j <= n; j ++ )
        {
            e[m ++] = {i, j, get_dist(points[i], points[j])};
        }

    printf("%.2lf\n", kruskal());

    return 0;
}