算法提高课汇总

$bellman\;ford\;?$

题目乍一看好像是有边数限制的最短路问题 — 可以用 $bellman\;ford$ 求解.

先简单回忆一下 $bellman\;ford$的算法过程:

• 程序循环$n$次, 每次遍历所有边, 判断三角不等式$dist[u]\le dist[v] + w(u, v)$是否成立, 更新所有
  点的最短路. 执行过程大致如下:

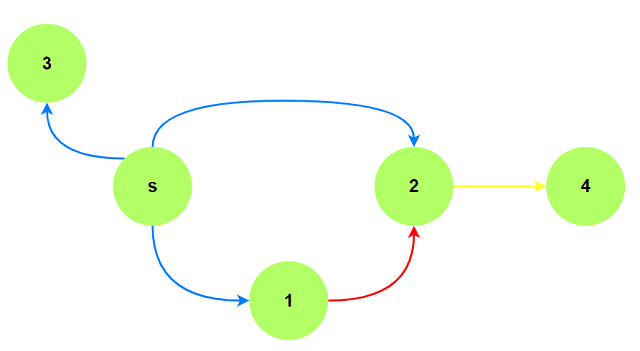
• 由于初始只有源点$s$的$dist = 0$, 所以第一次循环只有蓝色边连接的点会被更新; 第二次顶点$2$
  的距离可能被红色边更新; 第三次顶点$4$可能会被黄色点更新. 也就是在循环的第$k$次, 从起点经过
  $k$条边的顶点$u$的距离可能被更新. 之所以说“可能”是因为也许一个顶点在第$1$次更新就得到了从$s$
  到它的最短路. 所以 $bellman\;ford$ 算法只能求: 点$s$到点$u$的最多经过$k$条边的最短距离.

最多和恰好当然不是一回事, 所以这里$bellman\;ford$是不适用的. 不过顶点距离更新的思路值得我们借鉴.

类$floyd + $倍增思想

个人觉得本题更像是类 $bellman\;ford$ 算法的思想; $floyd$ 的更新形式; 加上类似快速幂的优化方式.

考虑从集合的角度考虑最值问题(注意与$floyd$状态定义的区别):

状态定义 $d(k, i, j)$

• 集合: 从$i$到$j$且经过路径边数为$k$的所有路径.

• 属性: Min路径权值和

状态计算

考虑将路径$i\rightarrow j$划分为独立的两个部分, 两个独立路径(没有条件依赖当然是独立的啦)的长度
分别是$a, b.$ 且$a + b == k$, 有$d(k, i, j) = min\lbrace d(a, i, u) + d(b, u, j)\rbrace, 1\le u\le n$.

也就是我们将$i\rightarrow j$拆分成两部分, 均取对应最小值:

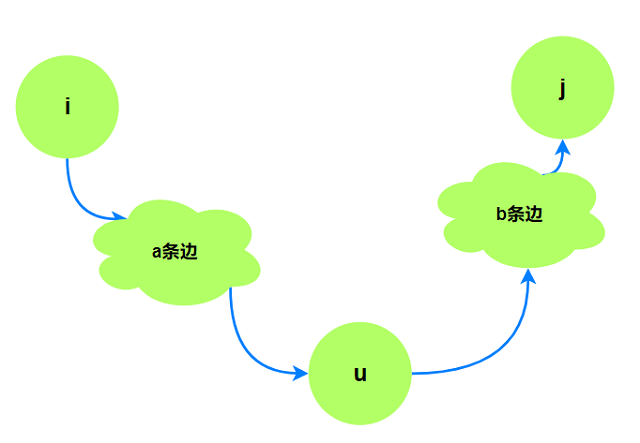
那么对于$d(k, i, j)$, 我们是否要遍历所有满足$a + b == k$的$a, b$以及中间顶点$u$呢?

由于$i\rightarrow j$的路径可以拆分为若干路径, 且任意路径间是没有条件依赖即相互独立的, 或者
说满足结合律: 计算的顺序任意. 可以采用快速幂的倍增思想优化计算过程.

快速幂优化

先简单回忆快速幂问题: 以$\lg(k)$的时间复杂度计算$a^k$: 由于乘法具有结合律, 可以考虑将
$k$拆分为二进制形式计算对应$a^{2^i}$快速求解. 例如$A^7 = AAAAAAA = A(AA)(AAAA)$.

在本题中每次倍增的对象是$d(k, i, j)$的路径数$k$: 路径数从$1\rightarrow 2\rightarrow … \rightarrow 2^i$.
我们可以用一个状态每次计算$d(2^k, i, j)$, 在$N$二进制对应1的部分将状态加入最终答案对应的状态中.

代码实现

细节注意

1. 离散化: 顶点最多$200$而顶点范围$1\sim 1000$, 需要用到离散化. 若不要求保序可以使用哈希值映射.

2. 在计算$d(k, i, j) = min\lbrace d(a, i, u) + d(b, u, j)\rbrace$过程中, $d(k, i, j)$的初始值
   应为$INF$而不能保存$k$之前状态的值. 在代码中体现为mul函数中的temp数组初始化$INF$,
   保证我们计算的是恰好经过而不是最多经过.

3. 代码中可以对$d(k, i, j)$做空间优化, 剩余代表路径长度的$k$维度. mul(res, g)实际上是$res[t,.,.]$
   与$g[2^i,.,.]$.

4. 因为在计算过程中需要考虑边数为1的自环, 所以邻接矩阵的初始化不能将自环设为$0$.

5. $sizeof + $数组而不是指针. 在数组作为参数传入函数时其有关大小的信息丢失了. 可以参考AcWing 341. 最优贸易 中的$memset$陷阱.

代码实现 $n^3\lg(n)$

#include <map>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 100 * 2 + 10; //边数 * 2

int n, m, k, S, E;
int g[N][N];
int res[N][N]; //记录最终状态

//a *= b
void mul(int a[][N], int b[][N])
{
    static int temp[N][N]; //暂存
    memset(temp, 0x3f, sizeof temp); //恰好而不是不大于 
    for( int k = 1; k <= n; k ++ ) //中间节点
        for( int i = 1; i <= n; i ++ )
            for( int j = 1; j <= n; j ++ )
                temp[i][j] = min(temp[i][j], a[i][k] + b[k][j] ); //优化空间后的状态计算
    memcpy(a, temp, sizeof temp); //注意sizeof + 数组 
}

void qmi()
{
    memset(res, 0x3f, sizeof res);
    for( int i = 1; i <= n; i ++ )  res[i][i] = 0; //零元 类似快速幂中res = 1

    while( k )
    {
        if( k & 1 ) mul(res, g); //res *= g
        mul(g, g);
        k >>= 1;
    }
}

int main()
{
    cin >> k >> m >> S >> E;

    map<int, int> id;
    memset(g, 0x3f, sizeof g);
    //for( int i = 1; i <= n; i ++ )  g[i][i] = 0; 自环也要考虑

    while( m -- )
    {
        int a, b, c;
        cin >> c >> a >> b;
        if( !id[a] )    id[a] = ++n;
        if( !id[b] )    id[b] = ++n;

        a = id[a], b = id[b]; //离散化
        g[a][b] = g[b][a] = min( g[a][b], c ); //不考虑重边 只保留最小边
    }

    qmi(); //快速幂优化

    cout << res[id[S]][id[E]] << endl;

    return 0;
}