算法提高课汇总

理解题意

• 至少包含3个点的环: 不考虑两点构成环的情况.

• 环上节点不重复: 实际上不需要额外考虑, 因为算法求长度最小的环, 而边权为正. 假设算法最优解
  的环中包含重复节点(多个环), 去掉重复节点构成的额外环一定会得到长度更小的环, 与最小环矛盾.

从集合的角度考虑最值问题

考虑集合划分: 以环上最大编号作为集合划分依据. 这样划分的好处是其思路与$floyd$类似: 算法中的$k$
每次都是递增的.

考虑我们已经计算完$d(k - 1, i, j)$, 还未计算$k$, 则一个包含$i, j, k$的环可以是:

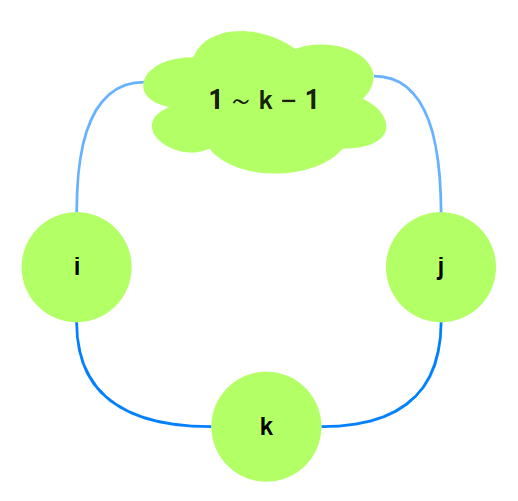
其中由$i\rightarrow j$中间只经过$1\sim k-1$的路径最短值由$floyd$计算: $d(k - 1, i, j)$,
所以包含$i, j, k$编号最大为$k$的环的最小值为: $w(i, k) + w(k, j) + d(k - 1, i, j)$.

遍历所有$k$对应环的最小值取最小即可.

直观理解: 为什么环可以这样构成?

• 因为对于环上编号均小于$k$的环, 若存在这样的环, 那么$k$一定与两个顶点相连, 而我们只要遍历所以的
  可能顶点即可.

求最小换方案

考虑 $floyd$ 的分析过程: 对于$d(k, i, j)$若包含顶点$k$, 则可以划分为独立的两个部分: $i\rightarrow k$
与$k\rightarrow j$, 考虑递归处理:

• 用$pos(i, j) = k$表示在$floyd$计算过程中$dis(i, j)$当前最小值的路径包含顶点$k$(由其更新而来).

• 若最优环的两个顶点为$i, j$: 可以每次记录其包含顶点$k$, 而对独立两条路径$i\rightarrow k$与$k\rightarrow j$
  用同样的方式递归处理, 得到各自的中间节点. 这里独立的含义是两条路径没有条件依赖, 各自取最小值即可.

代码实现

注意

1. 输出顺序任意的含义是你可以从环的任意一点沿着顺时针或逆时针输出, 但要注意其顺序一定是构成
   一个环的.例如$1\rightarrow 2\rightarrow 3\rightarrow 4$可以有多个输出顺序, 但不能输出$1\rightarrow 3\rightarrow 2\rightarrow 4$. 本题一种可能是顺序是: $1\sim k-1$(中间点)$\rightarrow j\rightarrow k\rightarrow i$.

2. 在每次更新环最小值时都需要找一次对应环上顶点, 而不能记录其$i, j, k$而在 $floyd$ 之后递归找环. 因为
   只有此时$d$与$pos$是符合其含义的, 而没有被后续的顶点更新.

3. 因为状态的限制, 在遍历一个包含$i, j, k$的环时$i, j\lt k$, 且最好满足$i\lt j\lt k$, 这样做的好处是保证
   环至少由3个顶点构成. 若将状态定义为除了$i, j$中间顶点经过最大顶点编号是$k$( $floyd$ 的遍历方式),
   则$i, j$每次需要遍历$1\sim n$, 需要额外考虑顶点重复的情况.

#include <cstring>
#include <iostream>

using namespace std;

typedef long long ll;

const int N = 110, INF = 0x3f3f3f3f;

int n, m;
int d[N][N], g[N][N];
int pos[N][N];
int path[N], cnt;

void get_path(int i, int j)
{
    if( !pos[i][j] )    return; //i -> j 中间没有顶点

    int u = pos[i][j];
    //注意添加顶点的顺序是按照i->j方向加入
    get_path(i, u); 
    path[++cnt] = u;
    get_path(u, j); 
}

int main()
{
    cin >> n >> m;

    memset(g, 0x3f, sizeof g);
    for( int i = 1; i <= n; i ++ )  g[i][i] = 0;

    while( m -- )
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min( g[a][b], c ); 
    }

    memcpy(d, g, sizeof g);
    int res = INF;
    for(int k = 1; k <= n; k ++ )
    {
        //遍历最大编号为k的环
        for( int i = 1; i < k; i ++ )
        {
            for( int j = i + 1; j < k; j ++ )
            {
                if( (ll)d[i][j] + g[j][k] + g[k][i] < res )
                { //(ll)(d+g+g)会出错
                    res = d[i][j] + g[j][k] + g[k][i];
                    cnt = 0;
                    get_path(i, j); //1~k-1 递归找i-j终点的顶点
                    path[++cnt] = j; path[++cnt] = k; path[++cnt] = i;
                }
            }
        }

        //floyd
        for( int i = 1; i <= n; i ++ )
            for( int j = 1; j <= n; j ++ )
            {
                if( d[i][j] > d[i][k] + d[k][j] )
                {
                    d[i][j] = d[i][k] + d[k][j];
                    pos[i][j] = k;
                }
            }
    }

    if( res == INF )    cout << "No solution.";
    else
    {
        for( int i = 1; i <= cnt; i ++ )    cout << path[i] << ' ';
    }

    return 0;
}