算法提高课汇总

传递闭包

不等式的传递性可以看作是顶点间的有向边, 问题可以转化为求传递闭包的问题.

啥是传递闭包

具体到图中, 可以认为是将间接传递关系变为直接传递关系(最小传递关系).

例如原图有如下传递关系:

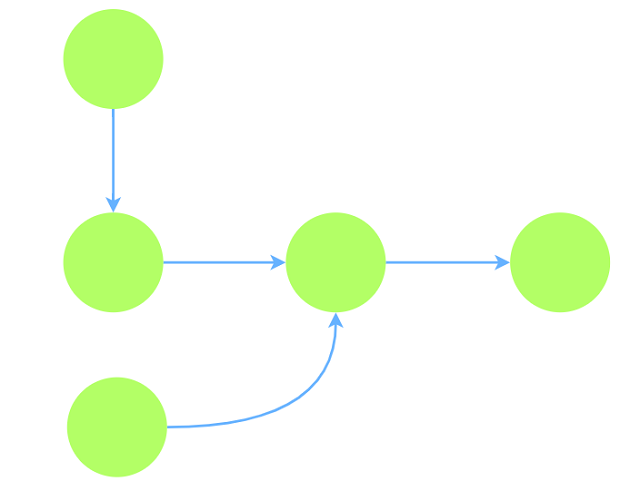
则其传递闭包为:

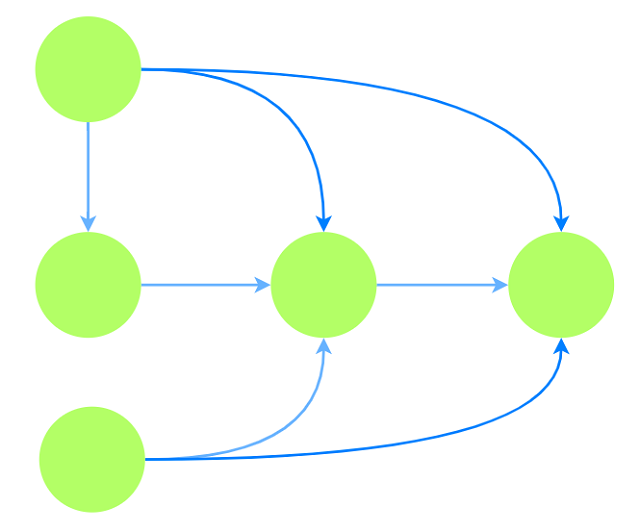
本题用传递闭包求解

我们用$A$到$B$的一条有向边表示$A\lt B$的关系.

• 关系全部确定: 任意两点间都存在一条有向边相连.

• 发生矛盾: 例如存在$A\lt B$, $B\lt A$的情况. 我们可以通过是否存在自环判断. 因为其闭包存在
  自己连向自己的边.

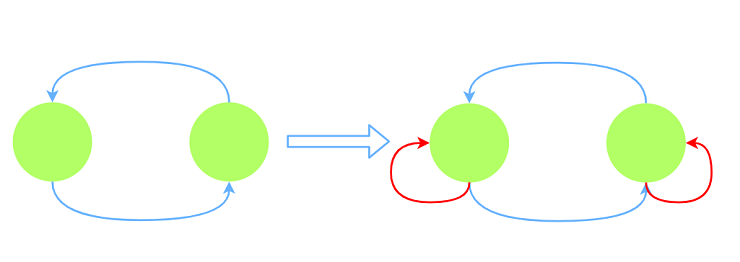
• 不能确定关系: 上述两种情况均未发生.

$Floyd$ 求解

实际上在 AcWing 1125. 牛的旅行 中我们就用到了类似的思路:

• 如果$d(i, j) = INF$, 则表明$(i, j)$不连通.

也就是通过$Floyd$算法可以得到$(i, j)$是否联通, 而在本题中可以认为是得到: 从$i$是否能连接到$j$.

或者我们也可以从$DP$的角度理解:

状态表示 $d(k, i, j)$

• 集合: 从$i$到$j$且只经过顶点$1\sim k$是否存在路径.

• 属性: Exist存在

状态计算

以路径是否包含顶点$k$作为划分依据:

• 不包含$k$: 则集合对应从$i$到$j$且只经过顶点$1\sim k-1$是否存在路径, 对应状态$d(k-1, i, j)$.

• 包含$k$: 路径划分为独立两部分: $i\rightarrow k$与$k\rightarrow j$. 存在$i\rightarrow j$的路径
  需要两个独立路径均存在. 对应状态: $d(k - 1, i, k)\&\&d(k - 1, k, j)$.

经过空间优化后, 状态计算公式为: $d(i, j) = d(i, j) \;||\; (\;d(i, k) \;\&\&\; d(k, j)\;)$.

代码实现

#include <cstring>
#include <iostream>

using namespace std;

const int N = 26;

int n, m;
bool g[N][N], d[N][N]; //g[u][v] = true: u < v
bool st[N]; //当前节点是否已经输出

void floyd()
{
    memcpy(d, g, sizeof g); //初始化
    for( int k = 0; k < n; k ++ )
        for( int i = 0; i < n; i ++ )
            for( int j = 0; j < n; j ++ )
                d[i][j] |= (d[i][k] & d[k][j]);
}

//返回0: 情况3; 1: 情况1; 2: 情况2
int check()
{
    for( int i = 0; i < n; i ++ )
        if( d[i][i] )
            return 2; //矛盾

    for( int i = 0; i < n; i ++ )
        for( int j = i + 1; j < n; j ++ )
        {
            if( !(d[i][j] | d[j][i]) ) //存在顶点关系未确定
                return 0;
        }
    return 1;

}

//找到当前还未输出的最小节点
char get_min()
{
    for( int i = 0; i < n; i ++ )
    {
        if( !st[i] )
        {//还未输出
            bool flag = true;
            for( int j = 0; j < n; j ++ )
            {
                if( !st[j] && d[j][i] )
                {//存在还未输出且小于i的顶点
                    flag = false;
                    break;
                }
            }
            if( flag )
            {
                st[i] = true;
                return 'A' + i;
            }
        }
    }
}

int main()
{
    while( cin >> n >> m, n || m )
    {
        memset(g, 0, sizeof g);
        int type = 0, t; //type: 0表示还未确定; t:迭代次数
        char s[4];

        for( int i = 1; i <= m; i ++ )
        {
            cin >> s;
            int u = s[0] - 'A', v = s[2] - 'A';
            g[u][v] = true; //u < v

            if( !type )
            {//仍未确定
                floyd();
                type = check();
                if( type )  t = i;
            }
        }

        if( !type ) puts("Sorted sequence cannot be determined.");
        else if( type == 2 )    printf("Inconsistency found after %d relations.\n", t);
        else
        {
            memset(st, 0, sizeof st);
            printf("Sorted sequence determined after %d relations: ", t);
            for( int i = 0; i < n; i++ )    printf("%c", get_min());
            printf(".\n");
        }
    }
    return 0;
}