算法提高课汇总

$Floyd$ 算法

基于$DP$计算多源汇最短路的算法.

$DP$ 分析

状态定义 $d(k, i, j)$

• 集合: 从$i$到$j$且中间只经过顶点$1\sim k$的所有路径.

• 属性: Min路径长度

状态计算

以$i$到$j$的路径中是否包含$k$作为划分依据.

• 不包含$k$: 此时对应集合 — 从$i$到$j$且中间只经过顶点$1\sim k - 1$的所有路径. 根据状态定义, 集合
  对应的路径长度最小值为$d(k-1, i, j)$.

• 包含$k$: 路径可以划分为独立的两个部分 — $i$到$k$与$k$到$j$. 为保持我们的Min属性, 两者都要取
  对应路径的最小值. 以$i$到$k$的路径为例, 对应集合 — 从$i$到$k$且中间只经过顶点$1\sim k - 1$的所有
  路径, 根据状态定义其最小值为$dp(k-1, i, k)$; 同理, 从$k$到$j$的最小值为$d(k - 1, k, j)$.

所以有$d(k, i, j) = min\lbrace d(k - 1, i, j), d(k - 1, i, k) + d(k - 1, k, j)\rbrace$.

因为$d(k,\cdot,\cdot)$仅依赖于$d(k - 1, \cdot, \cdot)$, 可以用背包空间优化的思路以$k$递增的顺序计算:

$\;\;\;\;d(i, j) = min\lbrace d(i, j), d(i, k) + d(k, j)\rbrace$.

状态初始化:

• $d(i, j) = 0\; if\; i == j$
• $d(i, j) = INF\;otherwise$

题意理解

• 牧区: 图的顶点.

• 牧场: 图的联通块.

• 直径: 联通块中任意两点距离的最大值.

在连接任意各属于不同连通块的两个点后:

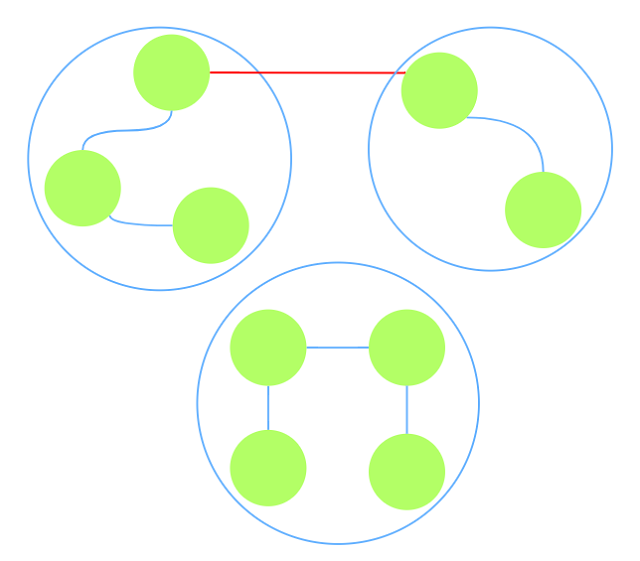
1. 连接前后原本连通块的直径不会减小, 所以连接后所有连通块最小值$res\ge max\lbrace d_i \rbrace$, 其中
   $d_i$表示原第$i$个连通块的直径.

2. 连接属于不同连通块的$u$, $v$后, 多出的一条可能直径的长度为$maxd(u) + maxd(v) + dist(u, v)$. 其中用
   $maxd(u)$表示顶点$u$与其所属连通块任意顶点距离的最大值; $maxd(v)$同理; $dist(u, v)$表示两点间距离.

用红色线表示连接后的可能的直径:

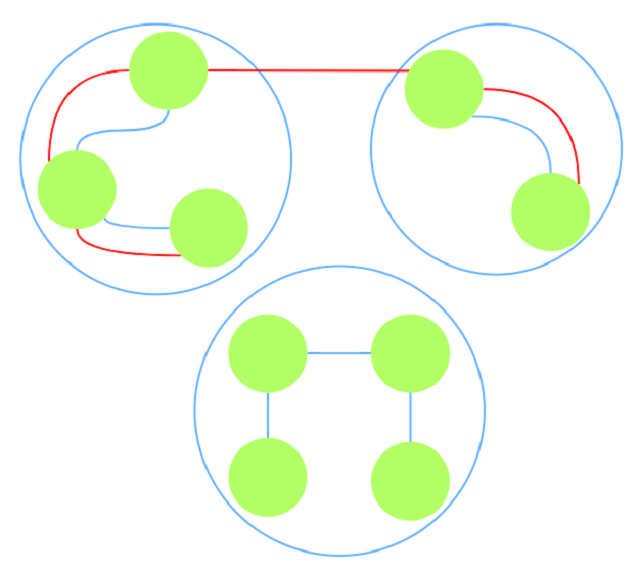
$Floyd$ 求解

注意本题提到的距离均指最短距离, 考虑用$floyd$先求解任意两个顶点的最短距离:

• 若$d(u, v) = INF$, 表示$(u, v)$不在同一连通块中.

• 否则, $d(u, v)$表示$(u, v)$间的距离(最短).

考虑$max\lbrace d_i \rbrace$的计算:

• 首先考虑$maxd(u)$的计算 — $u$与其所属连通块任意一点距离(最小距离)的最大值: 因为
  在通过$floyd$计算后,若$d(u, v) = INF$, 则说明它们不属于连通块, 所以
  $maxd(u) = max\lbrace d(u, v)\rbrace ,\;if\;d(u, v)\not=INF$, 即$u$与其联通块内顶点距离的最大值.

• 在计算所有$maxd(u)$后, 因为直径表示同一联通块内$maxd(u)$的最大, 而$max\lbrace d_i \rbrace$表示所有直径
  的最大, 所以其值等于$max\lbrace maxd(u) \rbrace$.

考虑任意两个不在同一连通块顶点连接后的可能直径:

• 即连接满足$d(u, v) = INF$的顶点, 其可能直径值为$maxd(u) + maxd(v) + dist(u, v)$.

枚举所有可能直径的最小值, 并取其与$max\lbrace d_i \rbrace$(由图确定的定值)的较大值即可.

代码实现

#include <cmath>
#include <iostream>

#define x first
#define y second

using namespace std;

typedef pair<int, int> pii;

const int N = 155;
const double INF = 1e20;

int n;
pii p[N]; //牧区坐标
char g[N][N]; //g[u][v] = '1' (u, v)有边相连
double d[N][N], maxd[N];

double get_dist(const pii &p1, const pii &p2)
{
    double dx = p1.x - p2.x, dy = p1.y - p2.y;
    return sqrt(dx * dx + dy * dy);
}

int main()
{
    cin >> n;
    for( int i = 0; i < n; i ++ )   cin >> p[i].x >> p[i].y;
    for( int i = 0; i < n; i ++ )   cin >> g[i];

    //floyd
    for( int i = 0; i < n; i ++ )
        for( int j = 0; j < n; j ++ )
        {
            if( i == j )    d[i][j] = 0;
            else
            {
                if( g[i][j] == '1' )    d[i][j] = get_dist(p[i], p[j]);
                else    d[i][j] = INF;
            }
        }

    for( int k = 0; k < n; k ++ )
        for( int i = 0; i < n; i ++ )
            for( int j = 0; j < n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

    //maxd的计算
    for( int i = 0; i < n; i ++ )
        for ( int j = 0; j < n; j ++ )
        {
            if( d[i][j] < INF )
            {//(i, j)联通
                maxd[i] = max( maxd[i], d[i][j] );
            }
        }

    double res1 = 0; //原图最长直径max{ maxd[i] }
    for( int i = 0; i < n; i ++ )   res1 = max( res1, maxd[i] );

    double res2 = INF; //连接顶点后的可能直径的最小值
    for( int i = 0; i < n; i ++ )
        for( int j = 0; j < n; j ++ )
        {
            if( d[i][j] >= INF )
            {//(i, j)不联通
                res2 = min( res2, maxd[i] + maxd[j] + get_dist(p[i], p[j]) );
            }
        }

    printf("%.6lf\n", max(res1, res2));

    return 0;
}