算法提高课汇总

$DP$求方案数

参考 AcWing 11. 背包问题求方案数 的思路: 用一个额外状态$cnt$记录从起点到顶点$u$的
最短路路径的方案数/路径数, 记录思路是如果从$v$到$u$的路径等于从起点到$u$的最短路径,
则通过$cnt[v]$更新$cnt[u]$.

$\;\;\;\;\;\;cnt[u] = \sum_v cnt[v], if\;dist[v] + w == dist[u]$

其中$dist$表示顶点的最短路径值(全局最小值).

用$DP$解决的问题可以转化为在拓扑图(即有向无环图)上求最值的问题(参考链接🔗 ), 而
在考虑图最短路径时不一定具有拓扑图的性质.

拓扑序

为何需要拓扑序

拓扑序保证在计算地点$u$的状态时, 其依赖的状态都更新完毕.

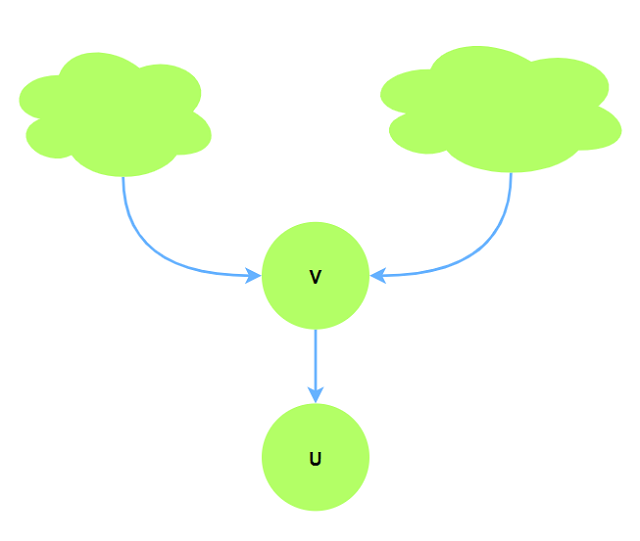
拓扑序保证在计算$v$状态时, 其之前依赖的状态已经更新完毕; 同理在计算$u$时, $v$也更新完毕.

而如果状态的更新顺序不是按拓扑序:

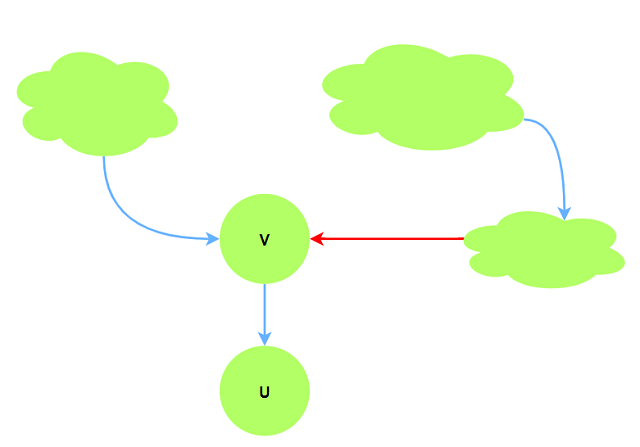
可能出现$v$由左边路径更新后更新$u$, 而实际上此时$v$的最短路径数还未更新完毕.

自带拓扑序算法

最短路的常见几个算法:

• $bfs$: 遍历顶点的顺序是拓扑序.

• $djkstra\;\&\;$双端队列$bfs$: 拓扑序.

• $bellman$_$ford\;\&\;spfa$: 不保证拓扑序, 可能会多次计算$dist[u]$.

算法计算顶点的顺序是否满足拓扑序的关键是在第一次使用$dist[v]$更新其他状态时就可以
保证$dist[v]$是最终的最短路, 即全局最小值, 保证之后不会再有其他顶点状态会回头更新
$dist[v]$. 所以我们在计算$cnt[u] += cnt[v]$时可以确保$cnt[v]$是一个最终的路径数(定值).

代码实现

无权图可以直接用带有拓扑序的$bfs$实现. 我们也可以用$spfa$实现: 先用$spfa$计算所有顶点的最短路径
的全局最小值, 再遍历图所有顶点, 利用$cnt[u] = \sum_v cnt[v], if\;dist[v] + w == dist[u]$求解.

• 最短路拓扑图: 只保留最短路径构成的有向无环图(权值均为正保证最短路中不存在环). 而$bfs$的拓扑序
  的含义就是其计算的顺序是按最短路拓扑图的顺序计算的; 而$spfa$一般情况不会按照其顺序遍历.

#include <cstring>
#include <iostream>

using namespace std;

const int N = 1e5 + 10, M = 2e5 * 2 + 10, mod = 100003;

int n, m;
int h[N], e[M], ne[M], idx;
int dist[N], q[N]; //bfs
int cnt[N];

void add(int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx ++;
}

void bfs()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0; cnt[1] = 1;

    int hh = 0, tt = 0; 
    q[tt ++] = 1;

    while( hh < tt )
    {
        int u = q[hh ++];//第一次也是最后一次用u更新其他顶点

        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v  = e[i];
            if( dist[v] > dist[u] + 1 )
            {
                dist[v] = dist[u] + 1;
                cnt[v] = cnt[u];
                q[tt ++] = v; 
            }
            else if( dist[v] == dist[u] + 1 )
            {
                cnt[v] = ( cnt[v] + cnt[u] ) % mod;
            }
        }
    }
}

int main()
{
    cin >> n >> m;

    memset(h, -1, sizeof h);
    while( m -- )
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    bfs();
    for( int i = 1; i <= n; i ++ )  cout << cnt[i] << endl;

    return 0;
}