整数划分

思路一

因为本题整数划分是不区分顺序的，所以抽象成一种完全背包

需要划分的整数$n$是一个容量为$n$的背包，可以用体积为$1$ ~ $n$的物品填充，这里一定要填满

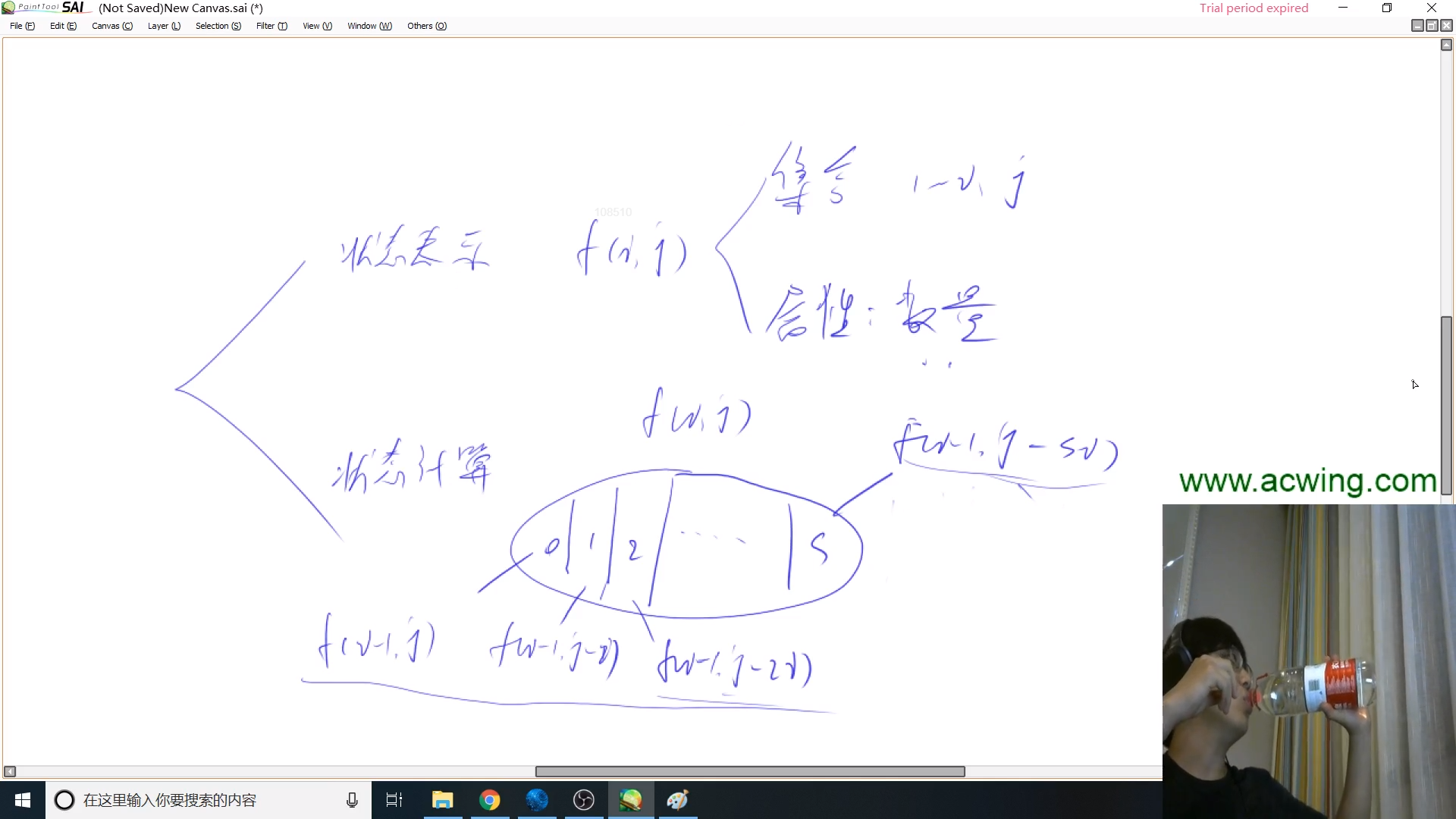
状态表示：$f[i][j]$

集合：用前$i$个数字凑成和位$j$的所有方案
属性：数量

状态计算

我们可以将f[i][j]按第$i$个数有多少个来划分

f[i][j] = f[i - 1][j - i] + f[i - 1][j - 2 * i] + f[i - 1][j - 3 * i] + f[i - 1][j - 4 * i] ...

类似完全背包

f[i][j] = f[i - 1][j - i] + f[i - 1][j - 2 * i] + f[i - 1][j - 3 * i] + f[i - 1][j - 4 * i] ...
f[i][j - i] =               f[i - 1][j - 2 * i] + f[i - 1][j - 3 * i] + f[i - 1][j - 4 * i] ...

对比可以得出状态转移方程

f[i][j] = f[i - 1][j] + f[i][j - i];

我们可以用滚动数组对它优化，因为是用到同层的数据，所以枚举从小到大枚举

f[j] = f[j] + f[j - i];

按照题目要求，我们最后需要对组合数字取模

初始化

和为0的时候，不管用前几种数字凑，都只有一种方案

for (int i = 0; i <= n; i ++ ) f[i][0] = 1;

滚动数组优化后的初始化

f[0] = 1;

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n;
int f[N];

int main()
{
    cin >> n;

    f[0] = 1; // 初始化，和为0的时候，有一种组合方法
    for (int i = 1; i <= n; i ++ )
        for (int j = i; j <= n; j ++ ) // 正序dp
            f[j] = (f[j] + f[j - i]) % mod; // 每次运算都要取模，防止溢出

    cout << f[n] << endl;

    return 0;
}

思路二

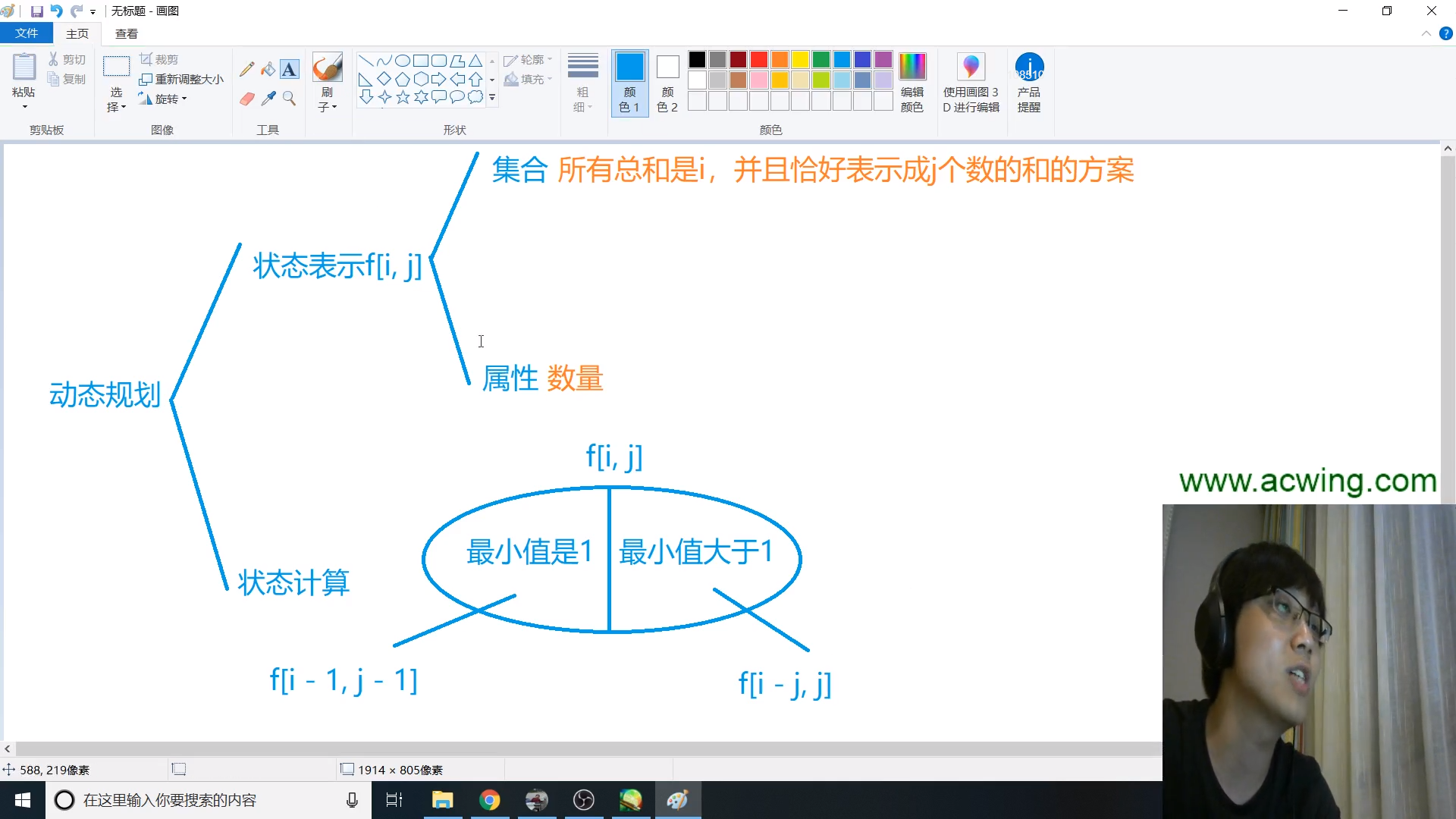
状态划分$f[i][j]$

集合：和为$i$并且能恰好划分成$n$个数的所有情况
属性：数量

状态计算

我们可以将发$f[i][j]$划分成最小值是1，和最小值大于1两种情况

最小值是1的情况下，我们去掉1，就是$f[i -1][j - 1]$的情况
最小值大于1，那我们每个数减去1，也不影响结果，就是f[i - j][j]

f[i][j] = f[i - 1][j - 1] + f[i - j][j];

$f[i][j]$表示的是和为$i$，划分成$j$个数的情况，所以最后要求一遍和

初始化

和为1，划分为1个数只有一种方案

f[1][1] = 1

我们从和为$2$开始计算，因为一个数字$n$，最多拆分为$n$个$1$所以第二层$j$最大就是$i$

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n;
int f[N][N];

int main()
{
    cin >> n;

    f[1][1] = 1; // 初始化
    for (int i = 2; i <= n; i ++ ) // dp
        for (int j = 1; j <= i; j ++ ) // 上线是i
            f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;

    int res = 0; // 将和为i拆分乘1 ~ n个数的情况加起来
    for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;

    cout << res << endl;

    return 0;
}