石子合并

思路分析

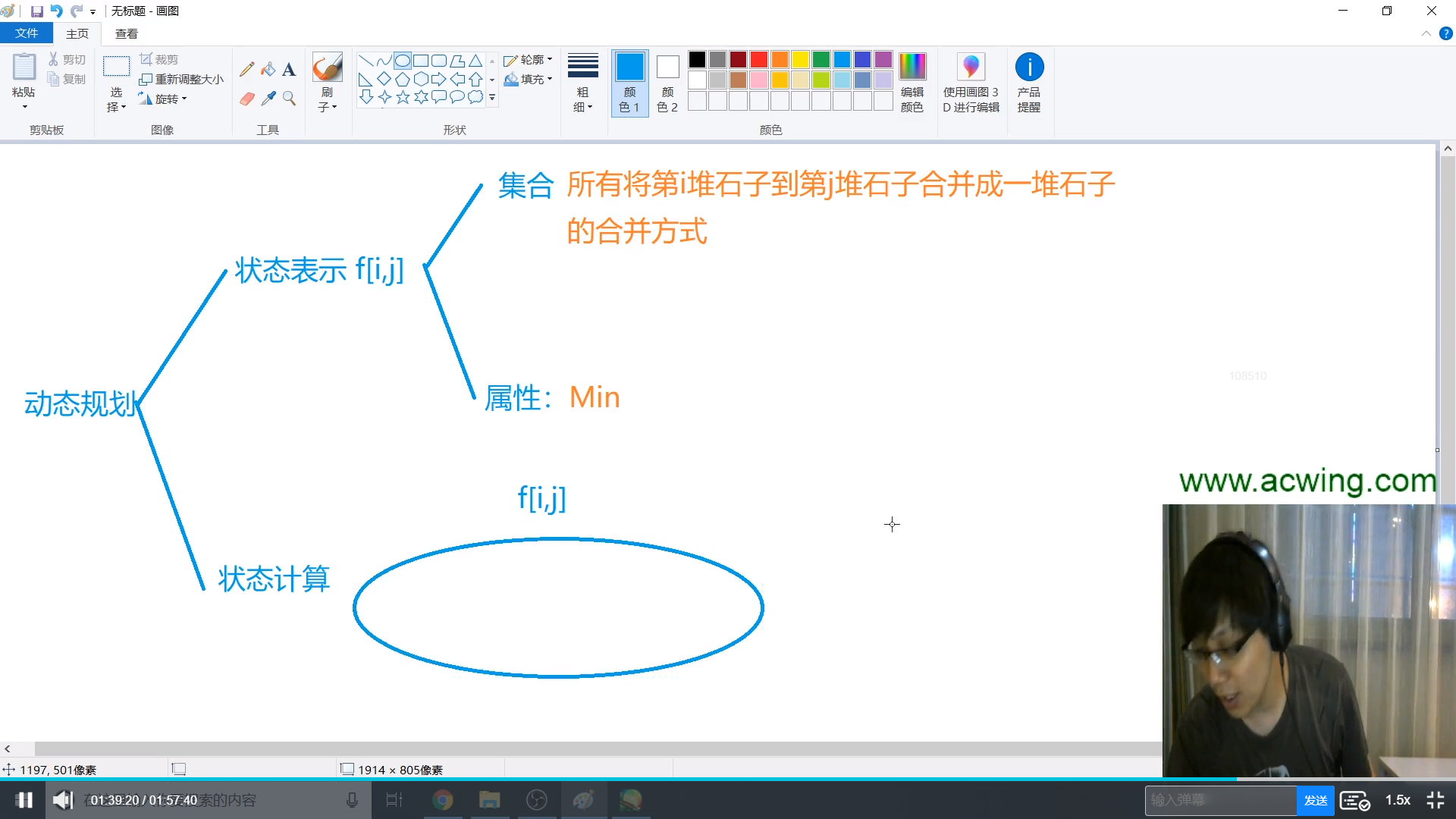
状态表示 $f[i][j]$

集合：将第$i$堆石子到第$j$堆石子合并的全部方式
属性：$min$，合并的最小花费

状态计算

这是一个简单的区间$dp$。首先，每次到最后一步，肯定是两堆石子合并成一堆。所以我们每次枚举划分结点，将一段范围划分成两个更小的范围，因为我们是从小到大计算的所以更小的范围一定被求解过了（或者直接记忆化搜索做）

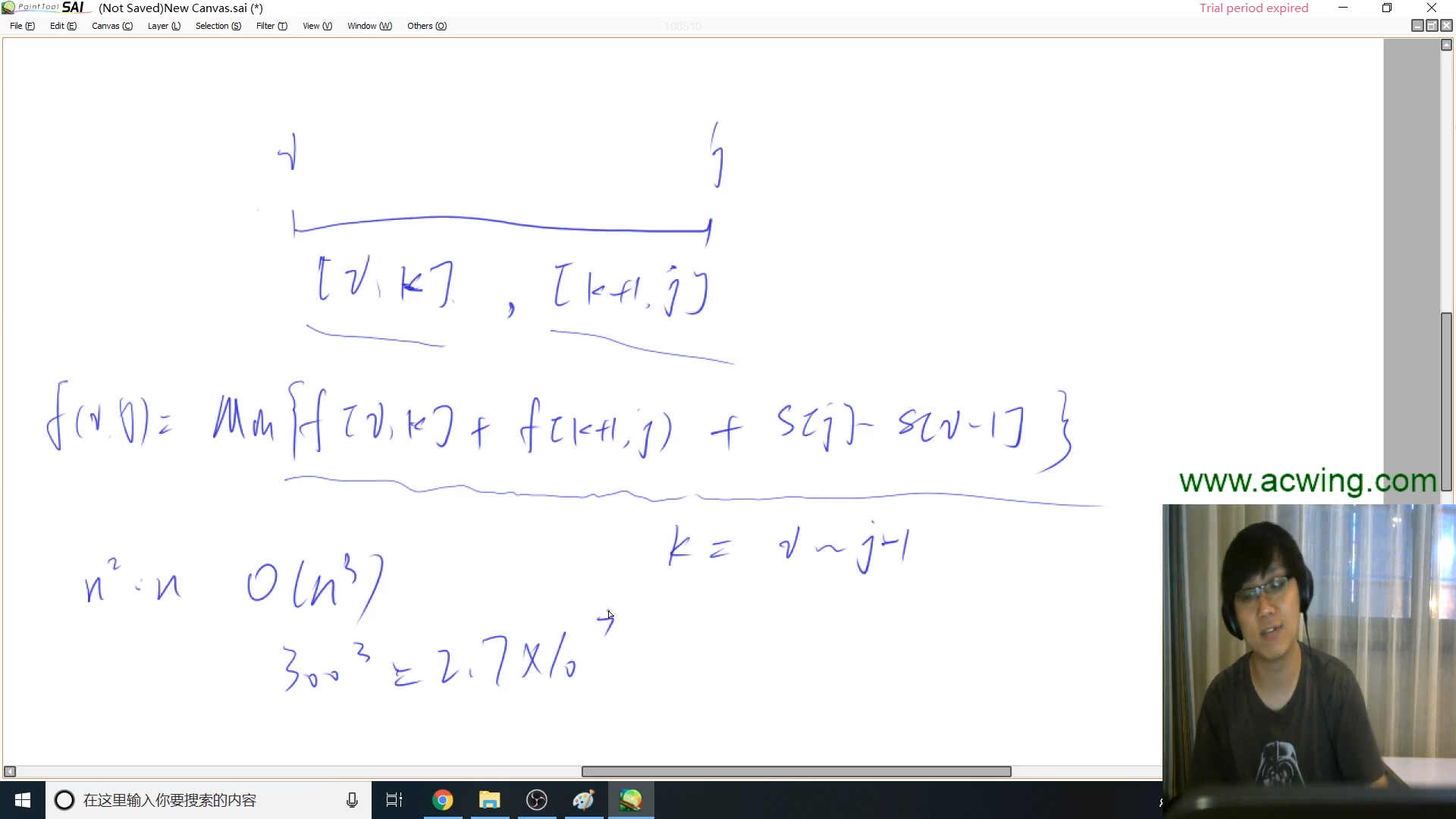
a[]是存储石子堆里石子个数的，f[][]是dp数组，k是i ~ j间的划分点
f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + a[i] + a[i + 1] + ... + a[j])

区间$dp$

最外层枚举区间长度，内层枚举左端点长度

对应该题，区间长度为$1$的石子堆，也就是不用合并，消耗的代价是$0$.所以最外层的区间长度从$2$开始，次外层枚举左端点，右端点编号就是左端点 $+ len - 1$，最内层考虑分割点

考虑分割点时候，分割点最左边是第一个石子堆的和第二个石子的间隔，我们让每一个石子堆右边的间隔的位置表示和当前石子堆一样。所以对于$i$ ~ $j$而言，分割点的范围是 $i$ ~ $(j - 1)$

因为每次取最小值，所以每次要给他赋一个比较大的值，要不然每次都是$0$

区间和优化

因为，我们这里要大量的计算一段区间的数字和
所以，利用第一章的区间和算法进行优化，提高效率

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 310;

int n;
int s[N]; // 区间和数组
int f[N][N]; // dp数组

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &s[i]);

    for (int i = 1; i <= n; i ++ ) s[i] += s[i - 1]; // 初始化区间和

    for (int len = 2; len <= n; len ++ ) // 区间dp， 枚举区间长度
        for (int i = 1; i + len - 1 <= n; i ++ ) // 枚举左端点
        {
            int l = i, r = i + len - 1; // 求出右端点
            f[l][r] = 1e8; // 初始化一个比较大的数，防止一直为0
            for (int k = l; k < r; k ++ ) // 枚举分割点
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]); // 利用区间和
        }

    printf("%d\n", f[1][n]);
    return 0;
}