最长公共子序列

思路分析

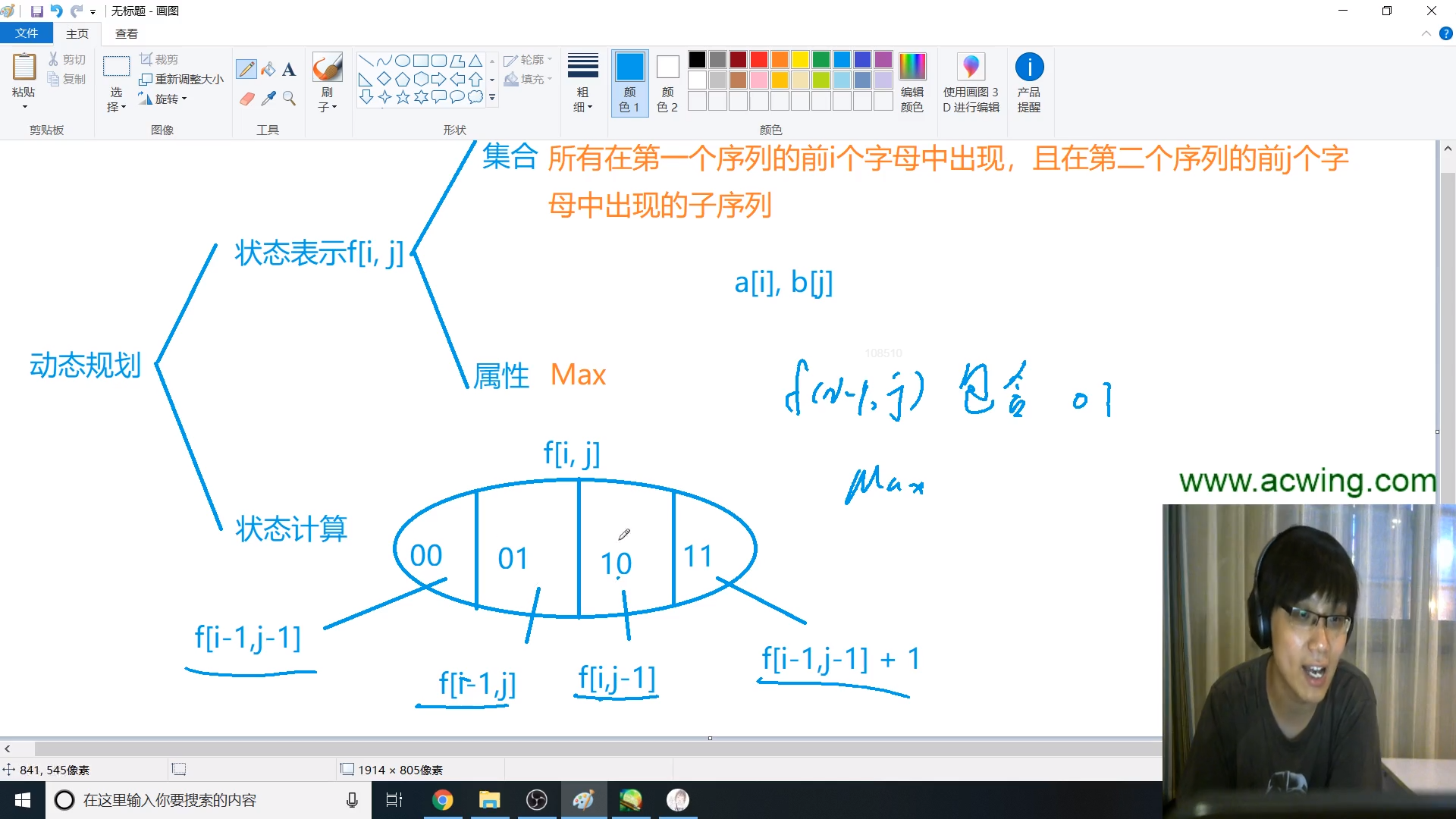
状态表示

$f[i][j]$， a[ ]是第一个字符串，b[ ]是第二个字符串
集合：所有在第一个字符串前i个字母中出现，并且在第二个字符串前j个字母中出现的子序列
属性： $max$

状态计算

划分是字符串最后一个字符在不在最长公共子序列里，所以有四种情况
1. 00：两个字符串的最后一个字母都不在
2. 01：a串最后一个字母不在，b串在
3. 10：a在，b不在
4. 11：两个字符串的最后一个字母都在里面

$(1)$ $00$
都不存在，那就都去掉

f[i][j] = f[i - 1][j - 1];

$(2)$ $11$
相当于最后一个字母都没有时候的最大值，再加上一个

f[i][j] = f[i - 1][j - 1] + 1;

$(3)$ $01$
我们本能会写出这样的式子

f[i][j] = f[i - 1][j];

但是它不对，因为$f[i - 1][j]$是a串前$(i - 1)$字母与b串前$j$个字母的最长公共子序列长度。这里是不一定包含b串的第$j$个字母

一个好的消息是，这个重复并不影响结果，因为这里求的是最大值，只要所有的情况不遗漏的考虑了就能求出争取的答案。三个属性，$max, min, cnt$。除了$cnt$是不允许重复的，$max$和$min$都允许重复

所以我们姑且用这个不太正确的式子来表示这种情况

$(4)$ $10$
这种情况和01一样，我们用范围更大的式子代表这种情况

f[i][j] = f[i][j - 1];

综合考虑上述四种情况，我们可以发现01,10两种也包含了00，因为$f[i - 1][j]$或者$f[i][j - 1]$都比$f[i - 1][j - 1]$多考虑了一个字母（$a[i]$或者$b[i]$）

对于任意一种情况，$f[i - 1][j]$ 和 $f[i][j - 1]$是一定存在的
所以先把这两种情况考虑下，如果$a[i] == b[j]$再考虑$11$的情况

f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);

另一种划分方式

所以我们分类标准其实是可以光看两个字符串最后两个字母是否相等

如果两字字符串的末尾相等，那么它就是在不考虑末尾情况下$+ 1$

如果这两个不相等，那么这两个字母不可能同时被纳入答案，那么我们单一考虑即可
等价于光考虑a串的最后一个字母在不在答案里面，或者考虑b串的最后一个字母，两个都不在的情况下，已经包含在上面两种情况的任意一种了。根据上面的分析，我们也可以知道这种划分方式也是存在重叠的

if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1] + 1;
else f[i][j] = max(f[i - 1][j], f[i][j - 1]);

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
    scanf("%d%d", &n, &m);
    scanf("%s%s", a + 1, b + 1); // 因为要-1，所以下标从1开始读

    for (int i = 1; i <= n; i ++ ) // dp过程
        for (int j = 1; j <= m; j ++ )
        {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]); // 先考虑都存在的情况
            if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1); // 相等的时候再考虑一种
        }

    printf("%d\n", f[n][m]); // 输出答案

    return 0;
}