最长上升子序列

思路分析

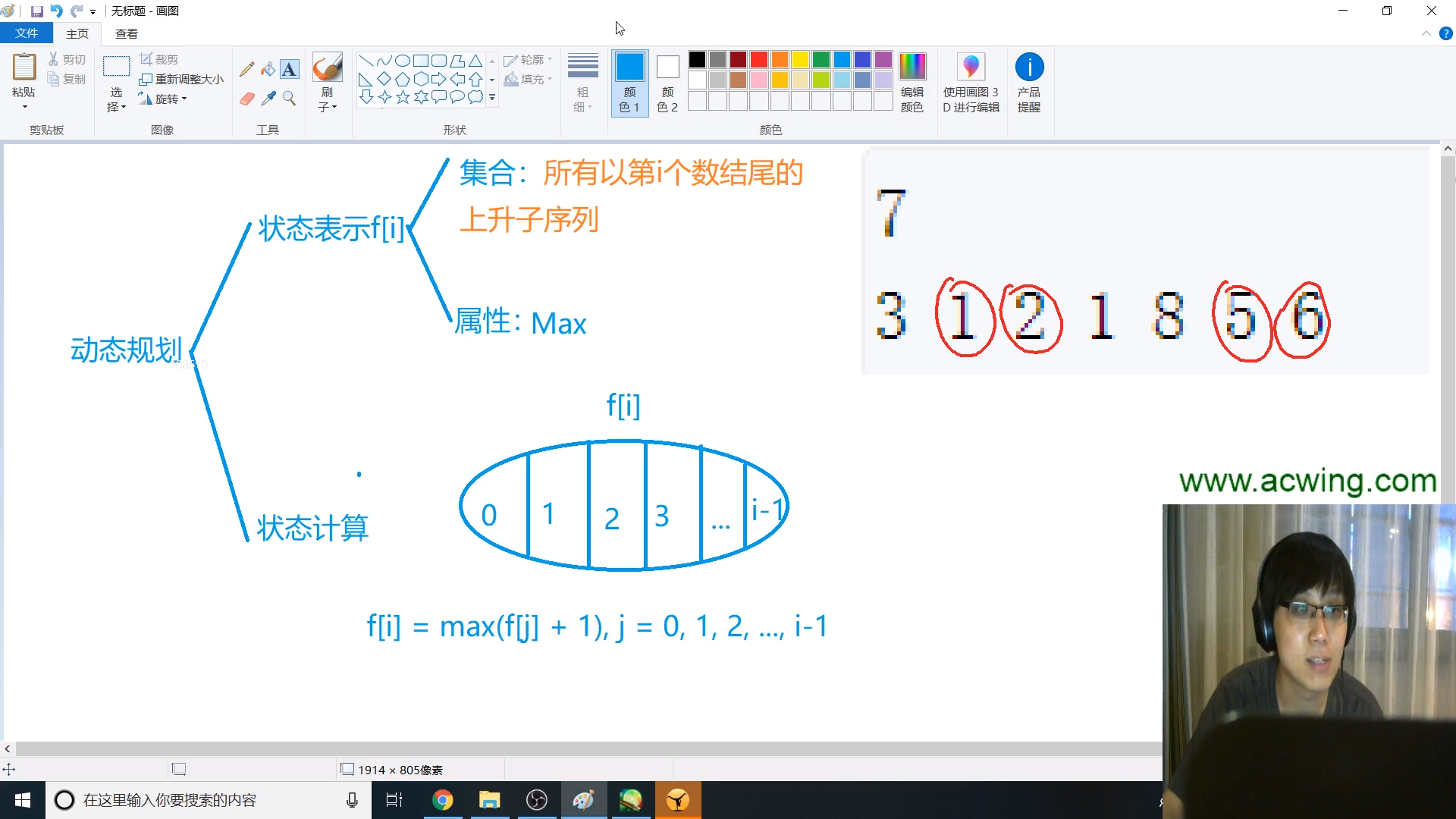
状态表示

$f[i]$表示以下标为$i$的数字结尾的上升子序列的集合

属性：子序列长度的最大值

状态计算

每次从前向后遍历，如果该点前面有点数值比它小，就试着更新一下

i表示当前点，j小于i也是下标
if (a[i] < a[j]) f[j] = max(f[j], f[i] + 1);

答案求解

因为我们最后求出的是以每一个点结尾的最长上升子序列，不是数组的。所以我们要遍历每一个数，找出数组里面的最长上升子序列

时间复杂度

动态规划的时间复杂度分析，可以用看循环层数的常规分析，也可以通过计算状态数量*每次转移的计算数量来求解

本题有$n$个状态，每次转移计算量也是$O(n)$， 所以时间复杂度是$O(n ^ 2)$。1000个数据，计算量$10 ^ 6$，$1s$内可以求解出来

记忆路径的动态规划

每次状态转移的时候记录下转移的上一个状态就行，多开一个等大的数组

y总代码这样最后是倒叙输出路径的，你也可以自己调整下正序输出

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int n;
int a[N], f[N], g[N]; // g[ ]是保存路径的数组

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1;
        g[i] = 0; // 如果前面没数字，下标为0，0在前面没有用过
        for (int j = 1; j < i; j ++ )
            if (a[j] < a[i])
                if (f[i] < f[j] + 1)
                {
                    f[i] = f[j] + 1;
                    g[i] = j; // 每次状态转移额外维护下路径
                }

    }

    int k = 1;
    for (int i = 1; i <= n; i ++ ) // 找到最长子序列的末尾数字
        if (f[k] < f[i])
            k = i;

    printf("%d\n", f[k]);

    // 逆序追踪
    for (int i = 0, len = f[k]; i < len; i ++ ) // 因为每轮k都在变化，所以在一开始把长度定下来
    {
        printf("%d ", a[k]);
        k = g[k];
    }
    return 0;
}

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n;
int a[N], f[N]; // a[ ]存数字， f[ ]是d数组

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]); // 读入

    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1; // 每一个点以它结尾子序列长度最小是1，也就是最差也是包含自己，不为0
        for (int j = 1; j < i; j ++ )
            if (a[j] < a[i]) // 如果前面的数字比它小就尝试着更新
                f[i] = max(f[i], f[j] + 1);
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[i]); // 遍历求解

    printf("%d\n", res);

    return 0;
}