数字三角形

思路分析

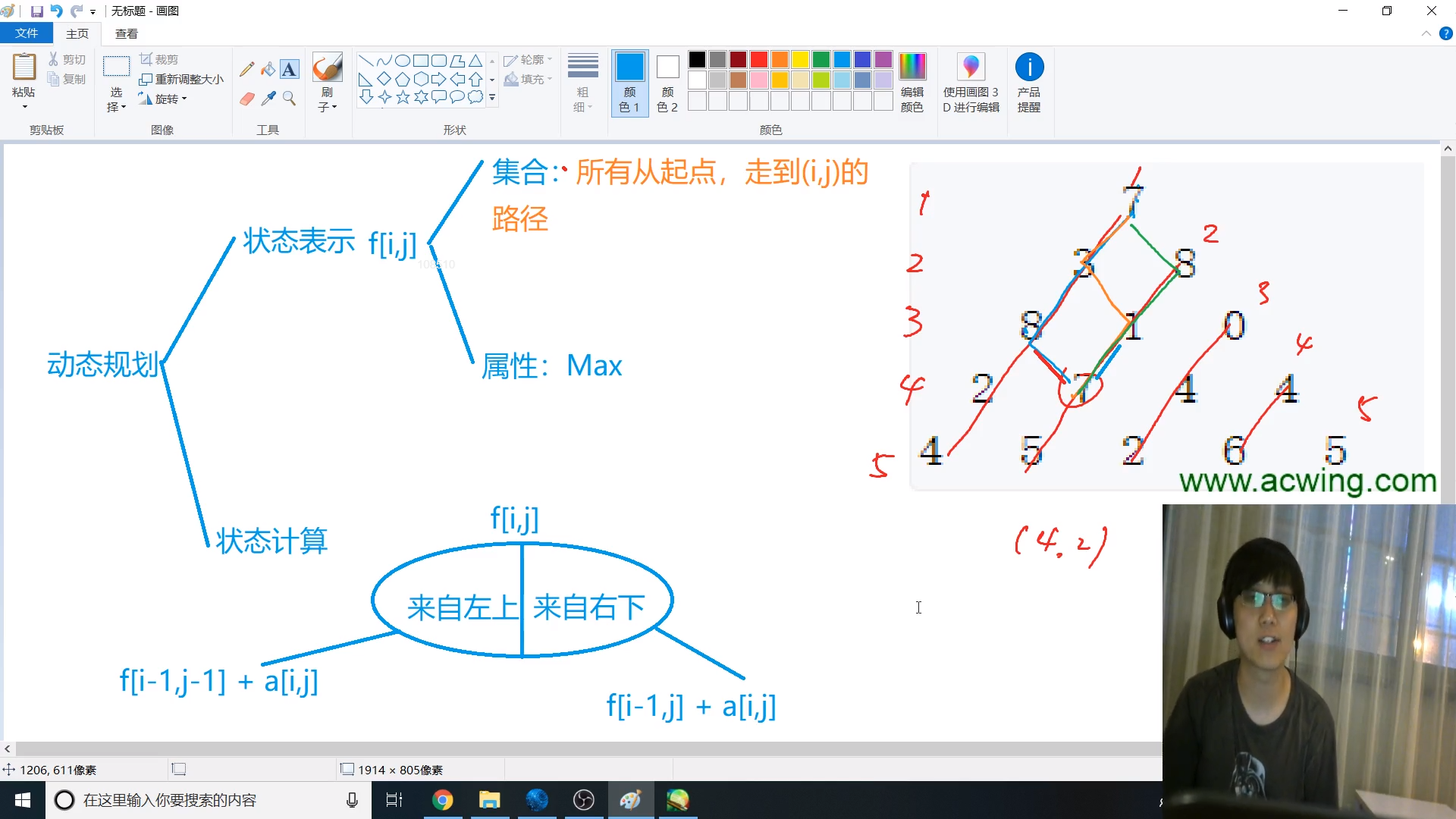
将数字三角形转化为二维数组

状态表示: $f[i][j]$

集合：所有从起点走到(i, j)点的路径
属性：经过数字和的最大值

状态计算

我们可以发现，任何一个点只会由左上方和右上方两个点（如果存在）转移下来

f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j]

因为下标里面有-1，所以我们下标要从1开始

初始化问题

首先数字三角形里面的数字范围是$-10000$ ~ $10000$，存在负数。所以对于不可达的路径求最大值，我们不能初始化为0，而要初始化为负无穷

我们计算需要用到的是从第$n$行的第0个到第$(n + 1)$个数字，所以初始化也要都初始化上

最后我们可以得到从起点到最后一行每一个点路径数字和的最大值，因为要求的是总最大值，所以我们对最后一行数字进行遍历求$Max$

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 1e9;

int n;
int a[N][N]; // 存数字三角形
int f[N][N]; // dp数组

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            scanf("%d", &a[i][j]); // 读入数据

    for (int i = 0; i <= n; i ++ )
        for (int j = 0; j <= i + 1; j ++ )
            f[i][j] = -INF; // 初始化

    f[1][1] = a[1][1]; // 第一个数字就是该点最短路径
    for (int i = 2; i <= n; i ++ ) // dp过程
        for (int j = 1; j <= i; j ++ )
            f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);

    int res = -INF;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]); // 求max

    printf("%d\n", res);
    return 0;
}