历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 1224. 交换瓶子原题链接中等

作者：

辰风 , 2020-01-27 13:47:18 , 所有人可见 , 阅读 7293

43

17

算法1

一

捕获.PNG

二

捕获1.PNG

三

捕获2.PNG

四

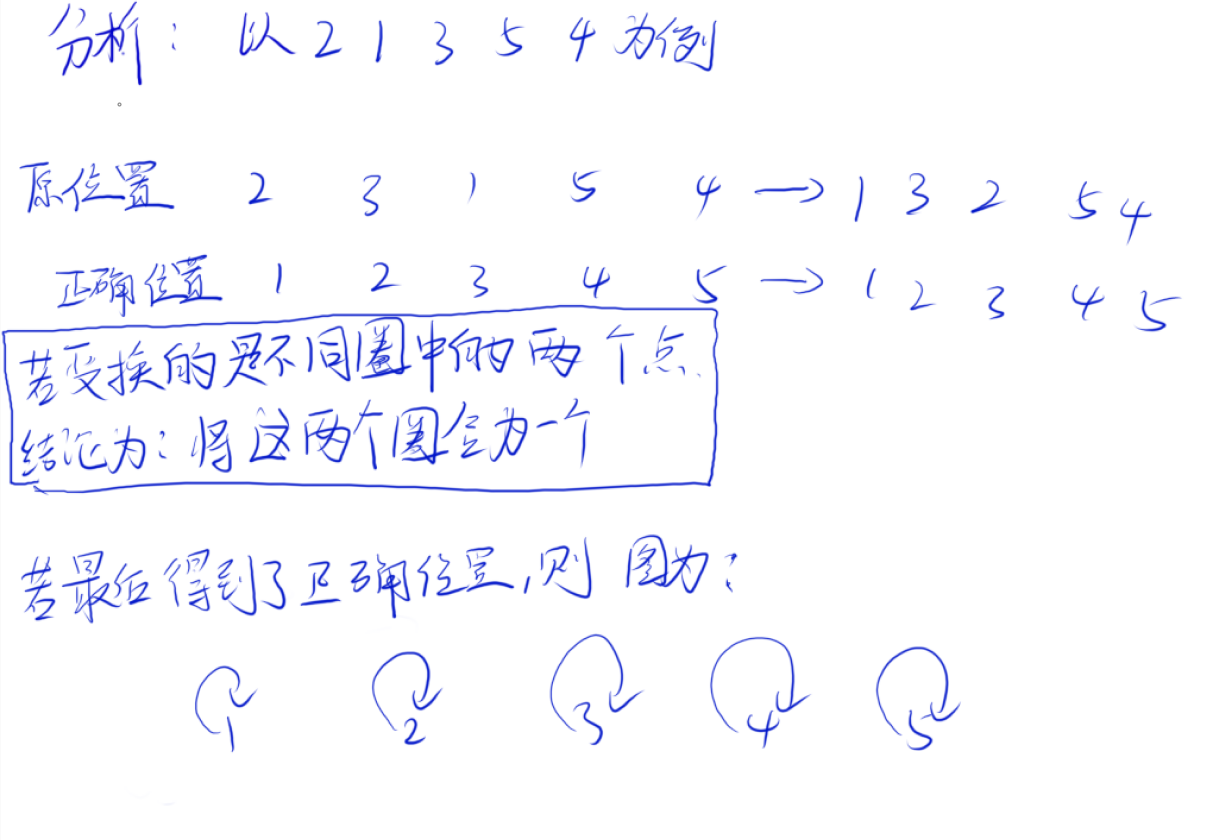
捕获3.PNG

五

捕获4.PNG

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=1e5+5;
int a[N];
bool st[N];
int main(){
    int n;
    cin >> n;
    for(int i=1;i<=n;i++){
        cin >> a[i];
    }
    int cnt=0;
    for(int i=1;i<=n;i++){
        if(!st[i]){
            cnt++;
            for(int j=i;!st[j];j=a[j]){//位置j指向a[j]的元素
                st[j]=true;
            }
        }
    }
    cout << n-cnt;
}

12 评论

please叫我叫兽 2022-03-29 21:52

少年补题王 2022-03-15 03:45

这个第四例有啥用。。。感觉图文不搭

fedfan 2020-10-11 10:41

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int n;
int s[10001];
int main() {
    int c = 0;
    scanf("%d",&n);
    for(int i = 1;i <= n;i ++) {
        scanf("%d",&s[i]);
    }
    for(int i = 1;i <= n;i ++) {
        while(s[i] != i) {
            c ++;
            //cout << s[i] << " " << s[s[i]] << endl; 
            swap(s[i],s[s[i]]);
            //for(int i = 1; i <= n; i ++) cout << s[i] << " ";
            //cout << endl;
        }
    }
    printf("%d",c);
}