算法提高课汇总

题意理解

从起点$1$出发到达终点$n$, 中途路径任意, 在经过某点时可以选择买入商品, 在之后经过的任意点
卖出, 通过不同点的差价赚取最大利润. 买卖最多进行一次, 不会做赔本生意.

$DP$分析

将从$1$到$N$的所有路径视为集合, 考虑集合划分方式: 以买入和卖出的分界点作为集合划分依据.

状态表示

$dmin(i)$

• 集合: $dmin(i)$ — 从起点$1$出发到达顶点$i$的所有路径.

• 属性: Min路径过程中买入的最低价格.

$dmax(i)$

• 集合: $dmax(i)$ — 从终点$N$出发反向到达顶点$i$的所有路径.

• 属性: Max路径过程中卖出的最高价格.

状态计算

以$dmin(i)$为例 — 假设从$1$到$i$的所有路径经过的点集为$v_1, v_2, …, v_k$,
$dmin(i) = Min\lbrace dmin(v_j), price_i\rbrace, 1\le j\le k$. 其中$price_i$为
在顶点$i$购买物品的价值.

问题求解转化为求以顶点$v$为界, 在其之前的顶点(包括$v$)买入, 在其之后的顶点(包括$v$)卖出
获得的最大价值. 即$res = Max\lbrace dmax(v) - dmin(v)\rbrace, 1\le v\le n$.

实际上本题不能直接用$DP$计算, 考虑存在环的情况:

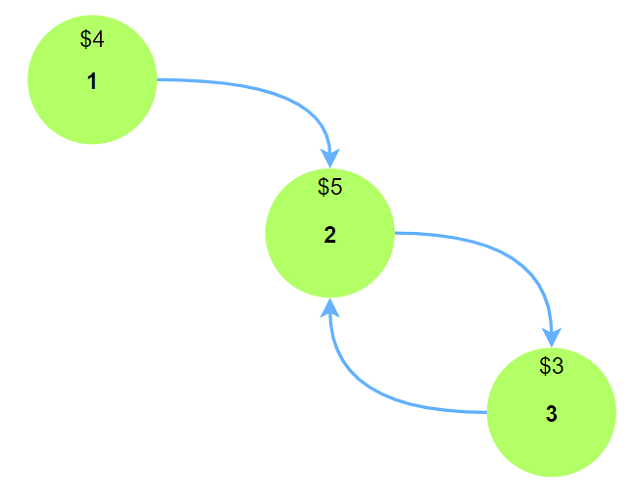
如果按照$DP$线性求解的方式, $dmin(2) = 4$而不是其对应状态定义的值: $3$.

我们可以依据$DP$分析状态的思路而采用最短路算法求解.

$DP$与图

如果将$DP$分析中的状态作为图中顶点, 状态之间的转移作为有向边, 则$DP$问题求解可以转换为图论
问题. 以$01$背包问题为例, 状态转移方程为$dp(i, j) = min\lbrace dp(i - 1, j), dp(i, j - v_i) + w_i\rbrace$:

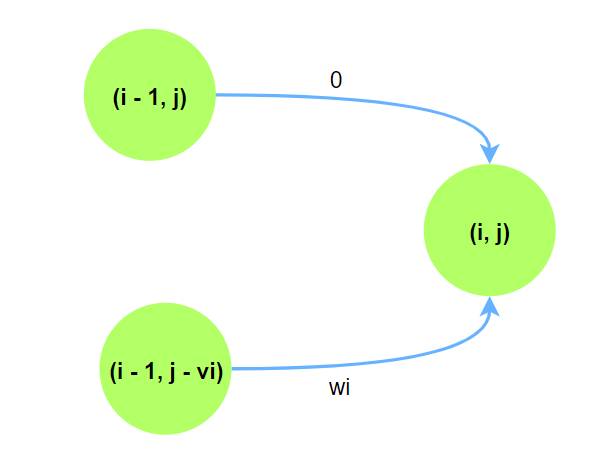
问题转化成起点为$dp(0, 0\sim m) = 0$, 终点为$dp(n, m)$的最长路径问题. 我们可以反向建图, 则问题
进一步转化为单源最长路径问题.

不过$DP$问题一般会转化为有向无环图(拓扑图)的最值路径问题. 当遇到环时, 一般我们可以利用$DP$
分析而用图算法求解.

单源最短路

以计算$dmin(i)$为例, 可以用单源最短路算法从起点$1$出发, 更新经过路径顶点的$dmin$值.

$dijkstra$不适用

$dijkstra$问题适用于边权为正的单源最短路问题, 算法正确性的关键是保证每次得到一个顶点的全局
最短路径值, 此后不会再被更新. 但本题略有不同, 不是求路径权值和, 而是求路径中顶点权值的最小值,
可能会遇到上图顶点$2$的情况, 所以此时$djkstra$不再适用. 而$spfa$算法会多次判断顶点$v$的$dist$值
是否能被更新, 所以这里可以用$spfa$而$dijkstra$不适用.

$memset$陷阱

$spfa$算法需要对距离数组做初始化, 然而如果直接对接受距离数组首地址的指针参数作为$memset$的
初始化参数$sizeof$时会出错: 实际程序只会对前$8$个字节做初始化. 原因是数组传入函数时其数组
长度的信息会丢失, 所以我们需要对$dmin\;\&\;dmax$做初始化. 参考连接🔗 .

$spfa$

#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 1e5 + 10, M = 5e5 * 2 * 2 + 10;

int n, m;
int hs[N], ht[N], e[M], ne[M], idx; //hs:正向 ht:反向
int price[N];
int q[N]; bool st[N]; //spfa
int dmin[N], dmax[N]; 

void add(int h[], int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx ++;
}

void spfa(int h[], int dist[], int type)
{
    int hh = 0, tt = 0;
    if( type == 0 ) //求dmin
    {
        memset(dist, 0x3f, sizeof dmin); 
        q[tt ++] = 1; //以1作为起点
        dmin[1] = price[1];
    }
    else
    {
        memset(dist, -0x3f, sizeof dmax);
        q[tt ++] = n;
        dmax[n] = price[n];
    }

    while( hh != tt )
    {
        int u = q[hh ++];
        if( hh == N )   hh = 0;

        st[u] = false;

        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( (type == 0 && dist[v] > min(dist[u], price[v])) || 
            (type == 1 && dist[v] < max(dist[u], price[v])) )
            {
                if( type == 0 )
                    dist[v] = min(dist[u], price[v]);
                else
                    dist[v] = max(dist[u], price[v]);
                if( !st[v] )
                {
                    st[v] = true;
                    q[tt ++] = v;
                    if( tt == N )   tt = 0;
                }
            }
        }
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for( int i = 1; i <= n; i ++ )  scanf("%d", &price[i]);

    memset(hs, -1, sizeof hs);
    memset(ht, -1, sizeof ht);
    while( m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(hs, a, b), add(ht, b, a);
        if( c == 2 )    add(hs, b, a), add(ht, a, b);
    }

    spfa(hs, dmin, 0);
    spfa(ht, dmax, 1);

    int res = 0; //0:至少不亏本
    for( int i = 1; i <= n; i ++ )  res = max( res, dmax[i] - dmin[i] );
    printf("%d\n", res);

    return 0;
}