算法提高课汇总

模型抽象

• 顶点: 城镇

• 边:

  • 道路: 双向边, 边权非负.
  • 航线: 单向边, 边权可负.
    $\;$
• 如果航线边$u$-->$v$, 则不存在路径使得从$v$到$u$: 航线连接的点不会形成环.

考虑由道路连接的点一定存在若干连通块: 如果存在道路$u$-->$v$, 由于是双向边则$v$-->$u$.
而题目要求航线连接的点不存在环, 那么在某个由道路组成的联通块内部一定不存在航线:

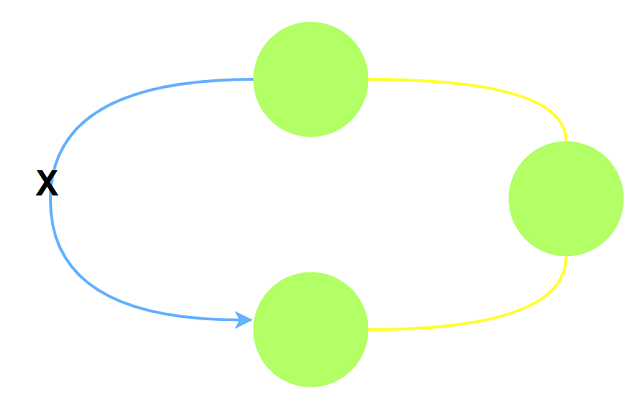
如果将每个由道路连接的联通块看作大顶点集合(团), 那么航线的两个顶点只能属于不同的团:

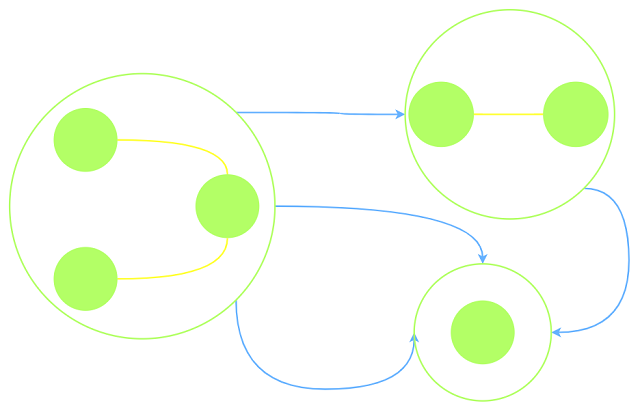
最短路

• 团内: 由于团内边权非负, 可以用$djkstra$计算.

• 团间: 将团作为顶点, 航线作为边, 则整个图为一个有向无环图, 可以得到一个拓扑序, 按拓扑序
  依次更新$s$到团内各点的最短路径.

代码实现

实现步骤

1. 计算顶点属于哪个团: 在仅用道路构成的图上使用$dfs$求得.

2. 团间拓扑序: 通过航线计算各团入度, 以团作为顶点计算团的拓扑序.

3. 团内最短路: 在团内使用$djkstra$算法, 需要判断更新顶点是否属于当前团: 若属于则将该顶点
   加入堆以更新团内其余顶点最短路; 否则更新其最短路, 并将对应团入度减$1$, 判断是否需要
   加入拓扑队列.

注意

• 图中存在负权边, 所以存在$INF < INF + (-w)$的情况, 即用不可达顶点也可以更新其他
  不可达顶点, 所以判断不可达顶点时其路径长度可能略小于初始的$INF$.

• 时间复杂度: $\sum_{bid} m_{bid}\lg(n_{bid})\lt \sum_{bid} m_{bid}\lg(n) = m\lg(n)$

#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>

#define w first
#define u second

using namespace std;

typedef pair<int, int> pii;

const int N = 25010, M = 50000 * 3 + 10, INF = 0x3f3f3f3f;

int n, mr, mp, s;
int h[N], e[M], w[M], ne[M], idx;
int id[N], bcnt = 0; vector<int> block[N]; //顶点团编号 团数目 以及团内顶点
queue<int> q; int din[N]; //拓扑队列 以及团入度
int dist[N]; bool st[N]; //dijkstra

void add(int u, int v, int c)
{
    e[idx] = v, w[idx] = c, ne[idx] = h[u], h[u] = idx ++ ;
}

void dfs(int u, int bid)
{
    id[u] = bid;
    block[bid].push_back(u);
    for( int i = h[u]; ~i; i = ne[i] ) //这里的边均是道路
    {
        int v = e[i];
        if( !id[v] )    dfs(v, bid);
    }
}

void dijkstra(int bid)
{
    priority_queue<pii, vector<pii>, greater<pii>> heap;
    for( int u : block[bid] )   
        heap.push({dist[u], u});

    while( heap.size() )
    {
        int u = heap.top().u; heap.pop();

        if( st[u] ) continue;
        else st[u] = true;

        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( dist[v] > dist[u] + w[i] )
            {
                dist[v] = dist[u] + w[i];
                if( id[u] == id[v] )    heap.push({dist[v], v}); //只加入团内顶点
            }
            if( id[u] != id[v] && --din[id[v]] == 0 )   q.push(id[v]); //更新其他团入度
        }
    }

}

void topsort()
{
    for( int i = 1; i <= bcnt; i ++ )
    {
        if( !din[i] )   q.push(i); //将入度为0的团加入拓扑队列
    }

    memset(st, 0, sizeof st);
    memset(dist, 0x3f, sizeof dist);
    dist[s] = 0; 
    while( q.size() ) //依次连续对团内顶点做djkstra 所以把初始化放在之前
    {
        int bid = q.front(); q.pop();
        dijkstra( bid );
    }
}

int main()
{
    scanf("%d%d%d%d", &n, &mr, &mp, &s);

    //道路建图
    memset(h, -1, sizeof h);
    while ( mr -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    //团
    for (int i = 1; i <= n; i ++ )
        if( !id[i] )    dfs(i, ++bcnt);

    //航线建图
    while ( mp -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c); 
        din[ id[b] ] ++; //更新入度
    }

    topsort();
    for( int i = 1; i <= n; i ++ )
        if( dist[i] > INF / 2 ) puts("NO PATH");
        else printf("%d\n", dist[i]);

    return 0;
}