算法提高课汇总

模型抽象

• 顶点: 各种物品. 终点为昂贵的聘礼.

• 边: 物品的交换(替代品)关系.

• 边权: 交换时物品的价值.

• 注意: “没必要用多样东西去换一样东西”: 只能用物品的一个替换品与之交换.

先不考虑等级关系, 以输入为例建图. 以红色箭头表明可以作为第一个购买的物品.

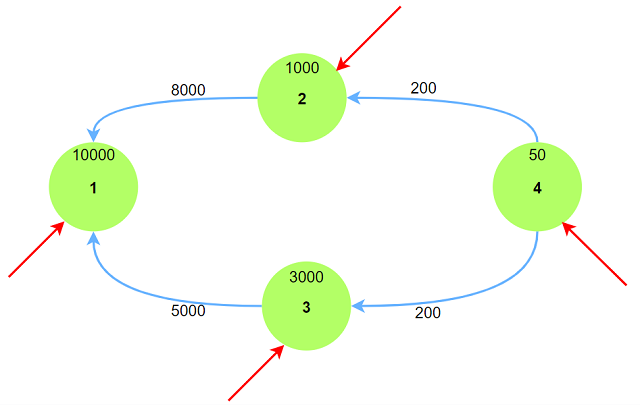
建图之后在计算时需要考虑两个问题:

1. 选择哪一个物品作为第一次购买的物品?

2. 需要为每个物品添加额外的价格属性, 在第一购买时加入总花费.

考虑在原图基础上加入一个虚拟源点$s$, 作为所有顶点的起点; $s$到物品的边权为物品的价格.
则上述两个问题在加入虚拟源点后不需要另外考虑:

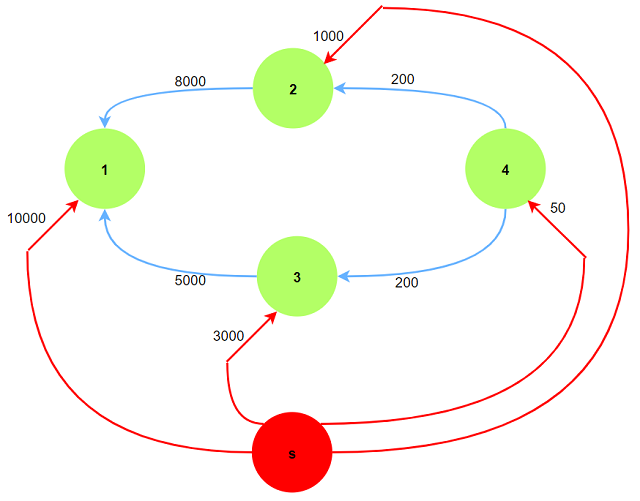
此时问题转化为从起点$s$到聘礼$1$的单源最短路问题.

另外需要考虑”间接交易”的等级的限制:

• 由于等级$1\le L\le 100$, 可以考虑枚举所有物品$1$所在的区间$[L, L + M]$, 从源点出发时, 只走
  在当前区间限制里的顶点. 取所有可能区间的最短路径的最小值即可.

代码实现

朴素$Dijkstra$

#include <cstring>
#include <iostream>

using namespace std;

const int N = 110, INF = 0x3f3f3f3f;

int m, n;
int level[N]; //level[i]: 物品i的主人的等级
int w[N][N]; //w[u][v]: 用u物品交换v所需要价值 若不存在则置为INF
int dist[N]; bool st[N]; //dijkstra

//考虑物品主任的等级在[lower, up]之间的交换后的聘礼的最小价值 返回最小价值
int dijkstra(int lower, int up)
{
    memset(st, 0, sizeof st);
    memset(dist, 0x3f, sizeof dist);
    dist[0] = 0;
    for( int i = 1; i <= n; i ++ )
    {
        int u = -1;
        for( int v = 0; v <= n; v ++ )
        {
            if( !st[v] && (u == -1 || dist[u] > dist[v]) )
                u = v;
        }

        st[u] = true;

        for( int v = 1; v <= n; v ++ )
            if( lower <= level[v] && level[v] <= up ) //只更新在区间内的物品
                dist[v] = min( dist[v], dist[u] + w[u][v] );
    }
    return dist[1];
}

int main()
{
    cin >> m >> n;

    memset(w, 0x3f, sizeof w);
    for ( int i = 1; i <= n; i ++ )
    {
        int price, cnt;
        cin >> price >> level[i] >> cnt;
        w[0][i] = price; //以0作为虚拟源点
        while ( cnt -- )
        {
            int t, v;
            cin >> t >> v;
            w[t][i] = min( w[t][i], v );
        }
    }

    int res = INF;
    for ( int l = level[1] - m; l <= level[1]; l ++ )
        res = min( res, dijkstra(l, l + m) );
    cout << res << endl;

    return 0;
}