题目描述

有 n 个城市，按从 0 到 n-1 编号。给你一个边数组 edges，其中edges[i] = [from_i, to_i, weight_i] 代表 from_i 和 to_i 两个城市之间的双向加权边，距离阈值是一个整数 distanceThreshold。

返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市，则返回编号最大的城市。

注意，连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。

样例

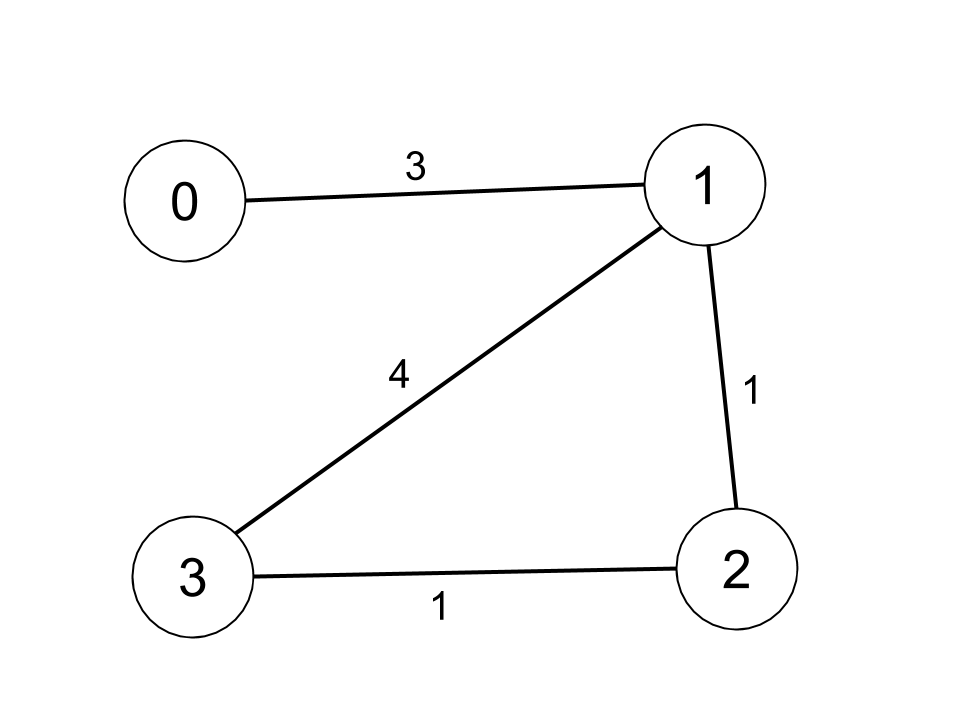
输入：n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出：3
解释：城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是：
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市，但是我们必须返回城市 3，因为它的编号最大。

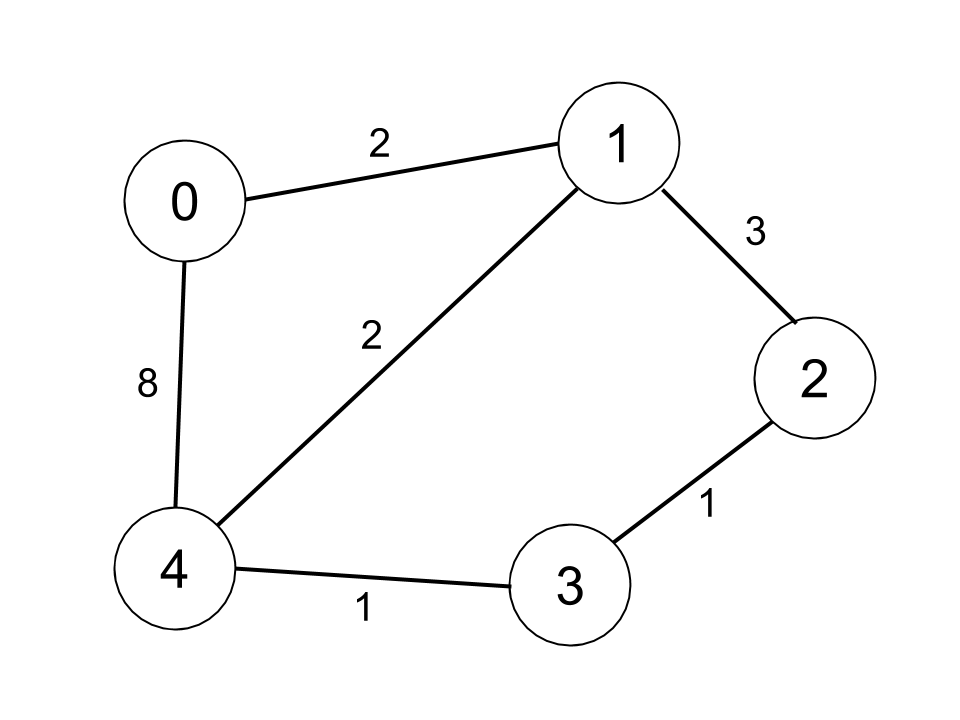
输入：n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出：0
解释：城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是：
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 4 以内只有 1 个邻居城市。

限制

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• 所有 (from_i, to_i) 都是不同的。

算法

(Floyd 最短路) $O(n^3)$

1. 利用 Floyd 算法求出任意两点间的最短路。
2. 枚举每个点，判断是否可以作为答案。

时间复杂度

• Floyd 求最短路的时间复杂度为 $O(n^3)$。
• 枚举一个点的时间复杂度为 $O(n)$，共有 $n$ 个点需要枚举。
• 故总时间复杂度为 $O(n^3)$。

空间复杂度

• 需要额外 $O(n^2)$ 的空间记录任意两点的距离。

C++ 代码

class Solution {
public:

    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        const int INF = 1000000000;
        vector<vector<int>> dis(n, vector<int>(n, INF));

        for (int i = 0; i < n; i++)
            dis[i][i] = 0;

        for (const auto &e: edges)
            dis[e[0]][e[1]] = dis[e[1]][e[0]] = e[2];

        for (int k = 0; k < n; k++)
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                    dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);

        int ans, c = INT_MAX;
        for (int i = 0; i < n; i++) {
            int t = 0;
            for (int j = 0; j < n; j++)
                if (dis[i][j] <= distanceThreshold)
                    t++;

            if (c >= t) {
                ans = i;
                c = t;
            }
        }

        return ans;
    }
};