题目描述

给你一个 m * n 的整数矩阵 mat，请你将同一条对角线上的元素（从左上到右下）按升序排序后，返回排好序的矩阵。

样例

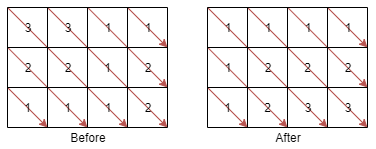
输入：mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
输出：[[1,1,1,1],[1,2,2,2],[1,2,3,3]]

限制

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• 1 <= mat[i][j] <= 100

算法

(暴力) $O((m + n)^2 \log (m + n))$

1. 按照对角线的顺序访问数组，然后对每个对角线排序。
2. 遍历时，先枚举差值，然后枚举行。根据行和差值计算列。

时间复杂度

• 共有 $O(m + n)$ 个对角线，每个对角线有 $O(m + n)$ 个元素。
• 故总时间复杂度为 $O((m + n)^2 \log (m + n))$。

空间复杂度

• 需要额外 $O(m + n)$ 的空间存储对角线元素用来排序。

C++ 代码

class Solution {
public:
    vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();

        for (int s = -n + 1; s <= m - 1; s++) {
            vector<int> tmp;

            for (int x = 0, y = x - s; x < m && y < n; x++, y++)
                if (y >= 0)
                    tmp.push_back(mat[x][y]);

            sort(tmp.begin(), tmp.end());

            for (int i = 0, x = 0, y = x - s; x < m && y < n; x++, y++)
                if (y >= 0)
                    mat[x][y] = tmp[i++];
        }

        return mat;
    }
};