算法提高课汇总

算法思路

考虑一种划分三角形的方式: 先确定多边形的两个点$(l, r)$, 其中$l\lt r$, 枚举顶点在$l\sim r$之间
的顶点$k$, 构成一个三角形. 由于题目限制三角形不能相交, 此时多边形被划分成三个部分:

• 🔺l-k-r

• 多边形: $l$ --> $l + 1 …$ --> $k$ --> $l$ 和$k$ --> $k + 1$ --> $r$ --> $k$.

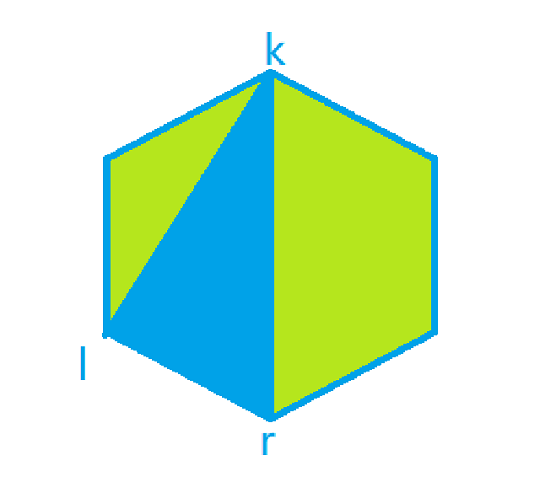
为便于理解以及划分更具有一般性, 下述划分也在我们这种划分方式的考虑范围内:

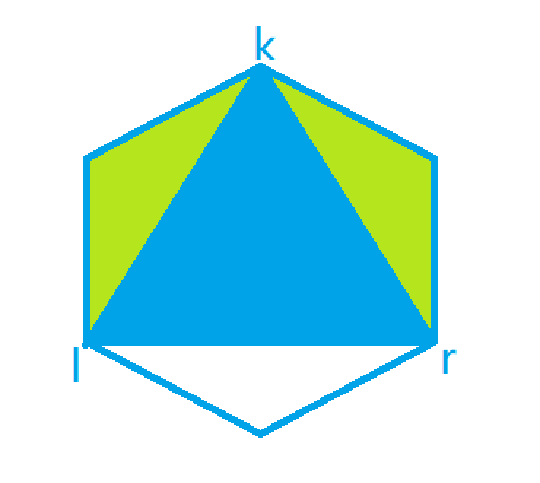
此时我们考虑的是多边形的一部分, 图中白色的部分没有考虑.

$DP$分析

状态表示$dp(l, r)$

• 集合: 将多边形$l$ --> $l + 1$ --> $r$ --> $l$划分为互不相交的三角形的所有方案.

• 属性: Min

状态计算

依据划分思路, 假设枚举的第三个顶点为$k$, $l\lt k\lt r$, 则这种划分方式对应权值为:

• 🔺l-k-r的权值: $w_l\times w_k\times w_r$.

• 两个子集对应的权值, 对于多边形$l$ --> $l + 1 …$ --> $k$ --> $l$, 根据状态的定义, 其代表集合
  将多边形$l$ --> $l + 1 …$ --> $k$ --> $l$划分为互不相交的三角形的所有方案对应权值的最小值, 即
  $dp(l, k)$; 同理多边形$k$ --> $k + 1$ --> $r$ --> $k$对应最小权值为$dp(k, r)$.

综上, $dp(l, r) = Min\lbrace dp(l, k) + dp(k, r) + w_l\times w_k\times w_r\rbrace$, $l\lt k\lt r$.

• 注意: 本题的计算公式与AcWing 320. 能量项链相同, 不同点在于本题考虑的是顶点集合, 顶点的顺序对于权值没有影响. 所以本题不是环形区间$DP$.

代码实现

本题由于权值的范围是$10^9$, 相乘后需要考虑高精度问题. 首先不考虑高精度, 实现上述思路的代码.

#include <iostream>

using namespace std;

const int N = 55, INF = 1e9;

int n;
int w[N];
int dp[N][N];

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> w[i];

    for( int len = 3; len <= n; len ++ )
    {
        for( int l = 1; l + len - 1 <= n; l ++ )
        {
            int r = l + len - 1;
            dp[l][r] = INF;
            for( int k = l + 1; k < r; k ++ )
                dp[l][r] = min( dp[l][r], dp[l][k] + dp[k][r] + w[l] * w[k] * w[r] );
        }
    }
    cout << dp[1][n] << endl;

    return 0;
}

高精度的一种实现可以参考链接🔗 .

#include <vector>
#include <iostream>

using namespace std;

typedef long long ll;

const int N = 55, M = 35;

int n;
ll w[N];
vector<int> dp[N][N];

//C = A + B
vector<int> add(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    int t = 0;
    for( int i = 0; i < A.size() || i < B.size(); i ++ )
    {
        if( i < A.size() )  t += A[i];
        if( i < B.size() )  t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if( t ) C.push_back(t);
    return C;
}

//C = A * b
vector<int> mul(vector<int> &A, ll b)
{
    ll t = 0;
    vector<int> C;
    for( int i = 0; i < A.size() || t; i ++ )
    {
        if( i < A.size() )  t += A[i] * b;
        C.push_back( t % 10 );
        t /= 10;
    }
    return C;
}

//A > B ?
bool cmp(vector<int> &A, vector<int> &B)
{
    if( A.size() != B.size() )
        return A.size() > B.size();
    for( int i = A.size() - 1; i >= 0; i -- )
        if( A[i] != B[i] )
            return A[i] > B[i];
    return false; // A == B
}

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> w[i];

    vector<int> temp;
    for( int len = 3; len <= n; len ++ )
    {
        for( int l = 1; l + len - 1 <= n; l ++ )
        {
            int r = l + len - 1;
            dp[l][r] = vector<int>(M, 1);
            for( int k = l + 1; k < r; k ++ )
            {
                temp.clear();
                temp.push_back( w[l] );
                temp = mul(temp,w[k] );
                temp = mul(temp,w[r] );
                temp = add(temp, dp[l][k] );
                temp = add(temp, dp[k][r] );
                if( cmp(dp[l][r], temp) )
                    dp[l][r] = temp;
            }
        }
    }

    for( int i = dp[1][n].size() - 1; i >= 0; i -- )    cout << dp[1][n][i];

    return 0;
}

或者可以采用数组实现.

#include <cstring>
#include <iostream>

using namespace std;

typedef long long ll;

const int N = 55, M = 35;

int n;
ll w[N];
ll dp[N][N][M];

// a += b
void add(ll a[], ll b[])
{
    static ll c[M];
    //memset(c, 0, sizeof c);
    for( int i = 0, t = 0; i < M; i ++ )
    {
        t += a[i] + b[i];
        c[i] = t % 10;
        t /= 10;
    }
    memcpy(a, c, sizeof c);
}

// a *= b
void mul(ll a[], ll b)
{
    static ll c[M];
    //memset(c, 0, sizeof c);
    ll t = 0;
    for( int i = 0; i < M; i ++ )
    {
        t += a[i] * b;
        c[i] = t % 10;
        t /= 10;
    }
    memcpy(a, c, sizeof c);
}

// a > b ?
bool cmp(ll a[], ll b[])
{
    for( int i = M - 1; i >= 0; i -- )
    {
        if( a[i] != b[i] ) 
            return a[i] > b[i];
    }
    return false; // a == b
}

void print(ll a[])
{
    int k = M - 1;
    while( k && a[k] == 0 ) k --;
    while( k >= 0 ) cout << a[k --];
}

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> w[i];

    ll temp[M];
    for( int len = 3; len <= n; len ++ )
    {
        for( int l = 1; l + len - 1 <= n; l ++ )
        {
            int r = l + len - 1;
            dp[l][r][M - 1] = 1; //dp[l][r] = 1000...0
            for( int k = l + 1; k < r; k ++ )
            {
                memset(temp, 0, sizeof temp);
                temp[0] = w[l];
                mul(temp, w[k]);
                mul(temp, w[r]);
                add(temp, dp[l][k]);
                add(temp, dp[k][r]);
                if( cmp(dp[l][r], temp) )
                {
                    memcpy(dp[l][r], temp, sizeof temp);
                }
            }
        }
    }
    print(dp[1][n]);

    return 0;
}