分组背包问题

思路分析

数据存储

$v[N][N]$和$w[N][N]$，第一维表示是第几组，第二维表示这一组里面的数据

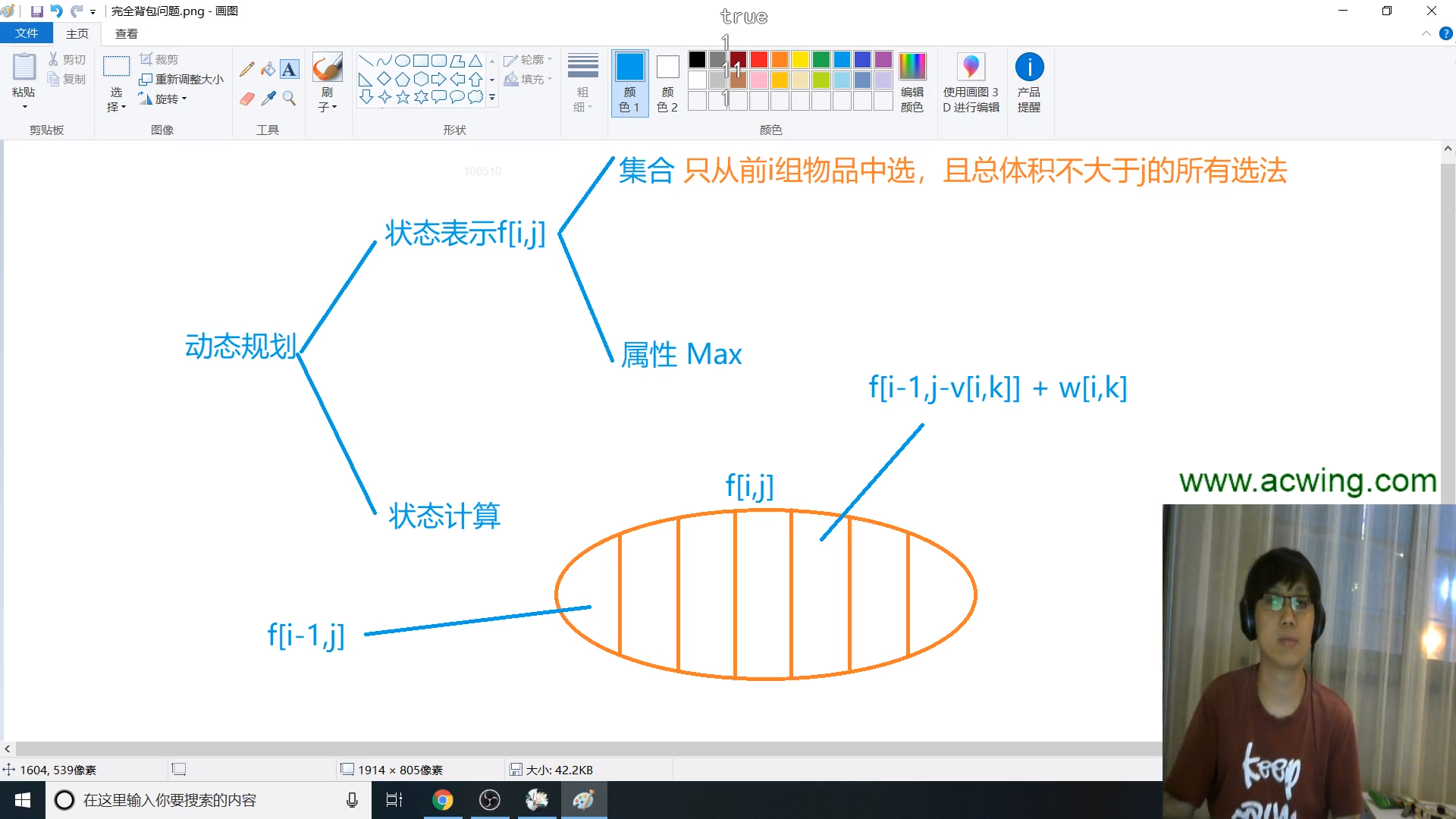
状态表示

$f[i][j]$表示前前$i$组中选物品，背包空间为$j$时候的最大价值

状态计算

这里，我们枚举每一组的每一个物品

$f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i][k]] + w[i][k])$

同样的，我们可以和之前一样运动滚动数组优化，因为是与上一个状态有关，所以倒叙列举

$i, j, k$顺序问题

$(1)$ $if$的判断条件不能放到$for$里面，因为$k$每一组物品的空间大小不是连续的
$(2)$ $i, j, k$不可以调换顺序，它们的顺序是由状态转移方程决定的，换了后意义就不存在了，纵使可以ac，但是那也是碰巧撞上的

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N]; // s[N]记录某一个组里面有多少个物品
int f[N]; // dp数组

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ ) // 读入数据
    {
        cin >> s[i];
        for (int j = 0; j < s[i]; j ++ )
            cin >> v[i][j] >> w[i][j];
    }

    for (int i = 1; i <= n; i ++ ) // dp
        for (int j = m; j >= 0; j -- )
            for (int k = 0; k < s[i]; k ++ )
                if (v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    cout << f[m] << endl;

    return 0;
}