多重背包问题 I

思路分析

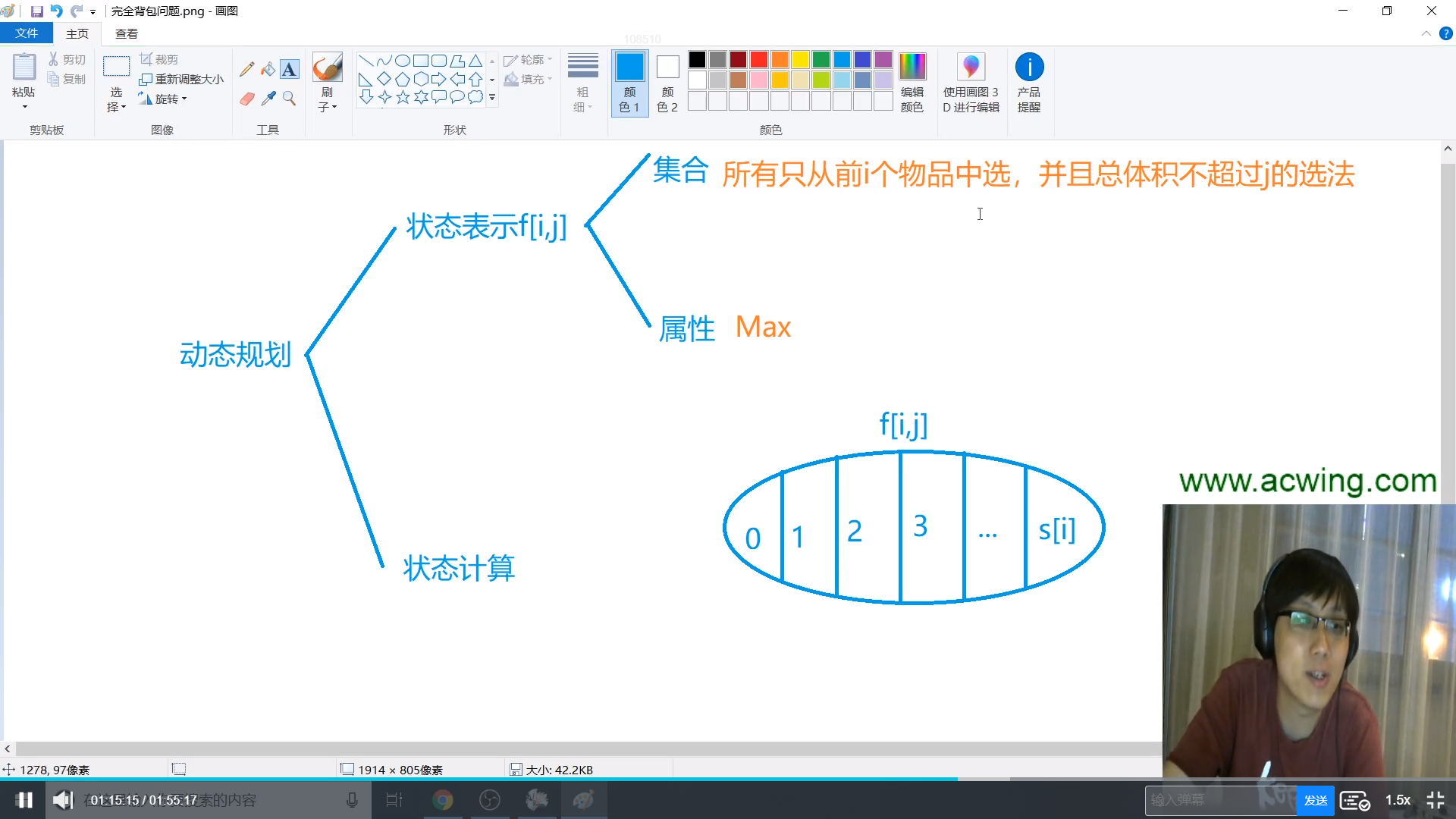
基础的思路是套用完全背包的朴素版算法，只是物品不是无限件，加一个物品数量的限制就够了

不能套用完全背包优化方法的原因是，由于物品数量的不确定性，我们不能保证$f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i] + w[i])$是正确的了

自引一下我的完全背包帖子：
https://www.acwing.com/solution/content/78550/

时间复杂度

最坏是$O(nm^2)$的，算一下是$10^6$，还可以计算出来

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N]; // 新增加的s[i]记录这个物品的件数
int f[N][N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i ++ ) // 类似完全背包的朴素写法
        for (int j = 0; j <= m; j ++ )
            for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ ) // 增加一个物品数量限制 
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);

    cout << f[n][m] << endl;
    return 0;
}