完全背包问题

思路分析

状态表示

$f[i][j]$表示只装前$i$个物品，背包体积为$j$能容纳的最大价值

状态计算

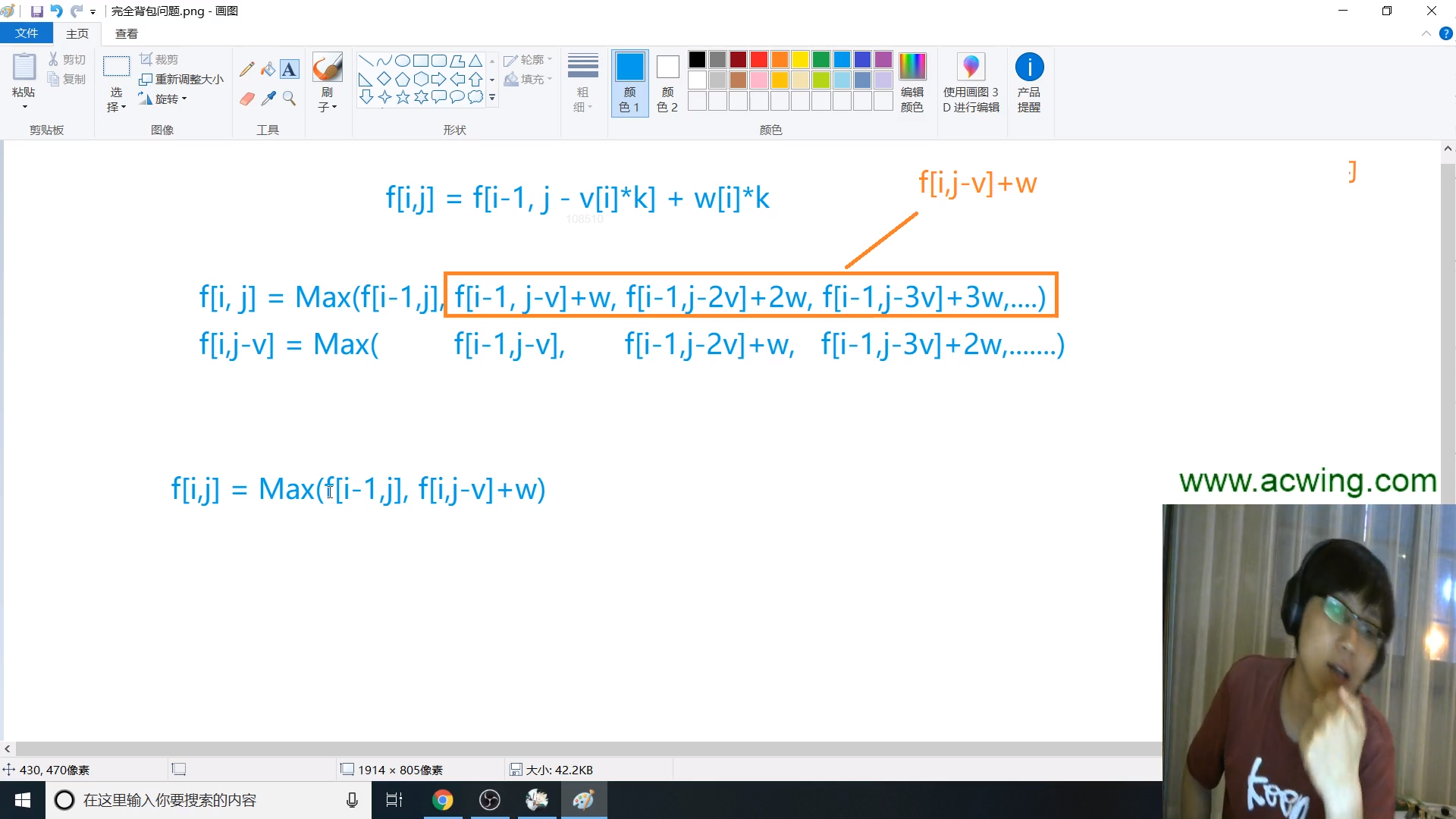
很明显，我们可以模仿01背包，考虑第$i$个物品不装，或者装一个，装两个......（如果装的下）

这样得到的状态转移方程为

f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i], f[i - 1][j - v[i]] + w[i], 
            f[i - 1][j - v[i] * 2] +w[i] * 2], .......)

这样的时间复杂度是很高的,$O(n m ^ 2)$

for (int i = 1; i <= n; i ++ )
    for (int j = 1; j <= m; j ++ )
        for (int k = 0; k * v[i] <= j; k ++ )
            f[i][j] = max(f[i][j],f[i - 1][j - v[i] * k] + w[i] * k);

我们可以看下$f[i][j - v[i]]$的状态划分情况

f[i][j - v[i] = max(f[i - 1][j - v[i]], f[i - 1][j - v[i] * 2] + w[i] * 1, 
                f[i - 1][j - v[i] * 3] + w[i] * 2..)

将它与$f[i][j]$相比，我们可以发现除去第$i$个物品一个不选的情况，剩下的每一项$f[i][j]$都比$f[i - 1][j - v[i]]$多一个$w[i]$
$f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]$

for (int i = 1; i <= n; i ++ )
    for (int j = 0; j <= m; j ++ )
    {
        f[i][j] = f[i - 1][j];
        if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
    }

同样的，我们可以发现，这一次，每一次的状态只与上一个状态有关，所以依然可以用滚动数组优化。
如果本次物品不选，那么就不变。剩下的是由本层状态转移来的，所以需要正序枚举

for (int i = 1; i <= n; i ++ )
    for (int j = 1; j <= m; j ++ ) // 正序写
        if (j >= v[i]) f[j] = max(f[j], f[j - v[i]] + w[i]);

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010; // 物品数量

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i]; // 读入

    for (int i = 1; i <= n; i ++ ) // 动态规划
        for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}