AcWing 1207. 大臣的旅费

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 1207. 大臣的旅费原题链接中等

作者：

小呆呆 , 2020-01-22 22:31:30 , 所有人可见 , 阅读 9578

55

31

算法分析1

由于题目说到不重复经过大城市，从首都到达每个大城市的方案都是唯一的。因此可以知道该图是一棵树，本题求的是树的直径

树的直径：树中长度最长的路径

1、任取一点x
2、找到距离x最远的点y
3、从y开始遍历，找到离y最远的点，与y最远的点的距离是树的直径

证明：y一定是树的直径的端点

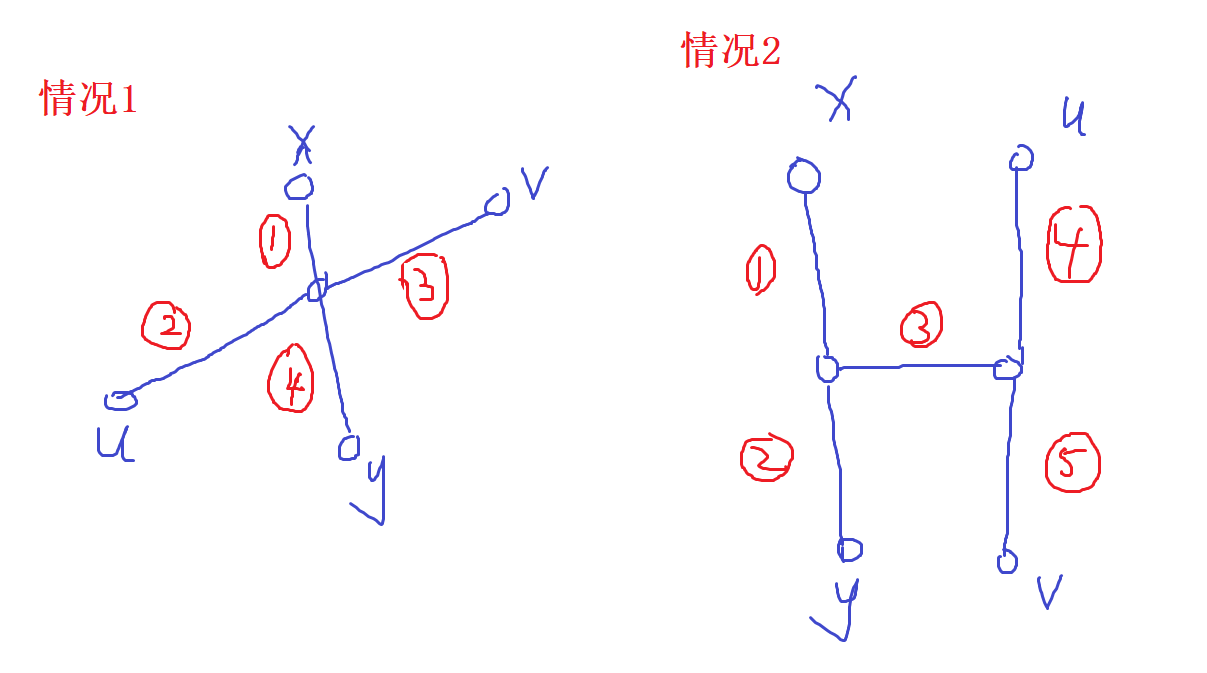
假设y不是树的直径的端点，分两种情况，如图所示，其中uv是树的直径

情况1：xy与uv有交点，由于离x最远的点是y，因此
- 有 1 + 3 <= 3 + 4
- 即 3 <= 4
- 则 3 + 2 <= 4 + 2
- 由于 3 + 2是树的直径，因此4 + 2一定是树的直径，因此y不是树的直径的端点矛盾
情况2:xy与uv没有交点，由于离x最远的点是y，因此
- 有 1 + 2 >= 1 + 3 + 5
- 即 2 >= 3 + 5
- 即 2 > 5
- 则 2 + 3 > 5
- 则 2 + 3 + 5 > 4 + 5
- 由于 4 + 5是树的直径，但存在着一个长度更长的路径，因此y不是树的直径的端点矛盾

因此，y一定是树的直径的端点

方法1

dfs

1、通过深度优先遍历找到与x的最远距离的点y
2、再通过深度优先遍历找到与y的最远距离

注意：递归函数需要记录上一结点father

时间复杂度 $O(n)$

参考文献

蓝桥杯辅导课

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main{
    static int N = 100010,M = 200010;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int[] w = new int[M];
    static int[] dist = new int[N];
    static int idx = 0;
    static void add(int a,int b,int c)
    {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    static void dfs(int u,int father,int distance)
    {
        dist[u] = distance;
        for(int i = h[u];i != -1;i = ne[i])
        {
            int j = e[i];
            if(j != father)
                dfs(j,u,distance + w[i]);
        }

    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        Arrays.fill(h,-1);
        for(int i = 0;i < n - 1;i ++)
        {
            int a = scan.nextInt();
            int b = scan.nextInt();
            int c = scan.nextInt();
            add(a,b,c);
            add(b,a,c);
        }
        //找到任意点x找到距离最远的点y
        dfs(1,-1,0);

        int u = 1;
        for(int i = 2;i <= n;i ++)
            if(dist[i] > dist[u])
                u = i;
        //找到离y最远的点的距离
        dfs(u,-1,0);
        int maxv = dist[1];
        for(int i = 2;i <= n;i ++)
        {
            if(dist[i] > maxv)
                maxv = dist[i];
        }

        System.out.println(maxv * 10 + ((long)(maxv + 1) * maxv ) / 2);
    }
}

方法2

bfs

1、通过广度度优先遍历找到与x的最远距离的点y
2、再通过广度优先遍历找到与y的最远距离

时间复杂度 $O(n)$

参考文献

蓝桥杯辅导课

Java 代码

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main{
    static int N = 100010,M = 200010;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int[] w = new int[M];
    static int[] dist = new int[N];
    static boolean[] st = new boolean[N];//判断该点是否被遍历过
    static int idx = 0;
    static void add(int a,int b,int c)
    {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    static void bfs(int u)
    {
        Queue<Integer> q = new LinkedList<Integer>();
        Arrays.fill(st, false);
        q.add(u);
        dist[u] = 0;
        st[u] = true;
        while(!q.isEmpty())
        {
            int t = q.poll();
            for(int i = h[t];i != -1;i = ne[i])
            {
                int j = e[i];
                if(st[j]) continue;
                dist[j] = dist[t] + w[i];
                st[j] = true;
                q.add(j);
            }
        }
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        Arrays.fill(h,-1);
        for(int i = 0;i < n - 1;i ++)
        {
            int a = scan.nextInt();
            int b = scan.nextInt();
            int c = scan.nextInt();
            add(a,b,c);
            add(b,a,c);
        }
        //找到任意点x找到距离最远的点
        bfs(1);
        int u = 1;
        for(int i = 2;i <= n;i ++)
            if(dist[i] > dist[u])
                u = i;
        //找到离y最远的点的距离
        bfs(u);
        int maxv = dist[1];
        for(int i = 2;i <= n;i ++)
        {
            if(dist[i] > maxv)
                maxv = dist[i];
        }

        System.out.println(maxv * 10 + ((long)(maxv + 1) * maxv ) / 2);

    }
}

算法分析2

树形dp

从任意结点开始，找到每个结点且经过该节点向下走的最大长度d1和次大长度d2，则经过该节点的最大长度是d1 + d2
dfs(u,father)表示找到u点往下走的最大长度d1

时间复杂度 $O(n)$

参考文献

算法提高课

Java 代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 100010;
    static int M = N * 2;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int[] w = new int[M];
    static int idx = 0;
    static int ans = 0;
    static void add(int a,int b,int c)
    {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    //找到u点往下走的最大长度
    static int dfs(int u,int father)
    {
        int d1 = 0;//最大值
        int d2 = 0;//次大值
        for(int i = h[u];i != -1;i = ne[i])
        {
            int j = e[i];
            if(j == father) continue;
            int d = dfs(j,u) + w[i];

            if(d > d1) {d2 = d1; d1 = d;}
            else if(d > d2) {d2 = d;}
        }
        ans = Math.max(ans, d1 + d2);
        return d1;
    }
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(reader.readLine().trim());
        Arrays.fill(h,-1);
        for(int i = 0;i < n - 1;i ++)
        {
            String[] s1 = reader.readLine().split(" ");
            int a = Integer.parseInt(s1[0]);
            int b = Integer.parseInt(s1[1]);
            int c = Integer.parseInt(s1[2]);
            add(a,b,c);
            add(b,a,c);
        }
        dfs(1,-1);
        System.out.println(ans * 10 + ((long)(ans + 1) * ans ) / 2);
    }
}