题目描述

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被计为是不同的子串。

示例 1:

输入: “abc”
输出: 3
解释: 三个回文子串: “a”, “b”, “c”.
示例 2:

输入: “aaa”
输出: 6
说明: 6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”.
注意:

输入的字符串长度不会超过1000。

算法1

(暴力枚举) $O(n^2)$

枚举每个回文子串的中心，然后计算每个中心的回文子串的个数。

时间复杂度

枚举中心的时间复杂度是$O(n)$,然后向外扩展的时间复杂度是$O(n)$,总体时间复杂度$O(n^2)$

C++ 代码

class Solution {
public:
    int palindrome(string s, int l, int r){
        int cnt = 0;
        while(~l && r < s.length()){
            if(s[l] == s[r]){
                l -- ;
                r ++ ;
                cnt ++ ;//如果相等则回文子串数+1
            }
            else break;
        }
        return cnt;
    }
    int countSubstrings(string s) {
        int n = s.size();
        int cnt = 0;
        int i = 0, j = 0;
        while(i < n && j < n){
            if(s[i] == s[j])
                cnt += palindrome(s, i, j);
            if(i == j) j ++ ;//两种子串中心
            else i ++ ;
        }
        return cnt;
    }
};

算法2

(manacher) $O(n)$

manacher算法就不详述了，有兴趣的可以百度一下，留一个算法的模板。
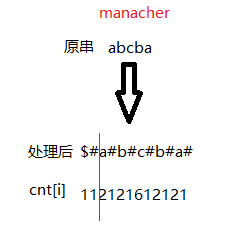
manacher算法将字符串的字符与字符之间插上’#’,比如说"abcba"=>"$#a#b#c#b#a#",然后计算每个字符的回文半径。如图所示。

回文中心的种类

回文字符串可分为两种，就是长度为奇数的或者长度为偶数的。举例来说"a","aba","abcba"这都是长度为奇数的回文字符串。"aa", "abba", "abccba"这都是长度为偶数的字符串。所以一个字符串中所有可能的回文字符子串的回文中心就可以分成2种，一个字母和两个字母。比如说”abbbba”，这个字符串可能的回文中心就有”a”,”ab”,”bb”,”b”,”bb”, “b”, “ba”, “a”.而在加工过后的字符串中”#”就代表了以两个字母为回文中心的子串。例如”#a#b#b#a#”，最中间的”#”,就代表了以“bb”为中心的回文子串。

cnt[i]表示什么

那么cnt[i]表示什么呢？这里直接给答案，cnt[i]表示的是S[i]对应的回文中心的回文字符串的长度加1.比如在图中的红线后面，第一个字母a对应的cnt[2] = 2,就表示在字符串”abcba”中，以第一个字母a为中心的回文字符串的最大长度是2 - 1 = 1;也就是字母a本身。同样的，我们再看最中心的’c’,他对应的cnt = 6,那么在字符串”abcba”中，以’c’为中心的回文子串最大长度就是6 - 1 = 5。也就是”abcba”本身。因为这个串里面没有连续的两个字母是相等的，所以所有’#’对应的cnt都为1，也就是长度为1 - 1 = 0，不构成回文字符串。

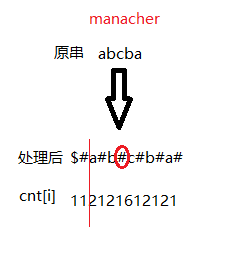
我们可以换一个例子’abba’,加工后为’$#a#b#b#a#’,那么第三个‘#’对应的cnt = 5,所以以字符串中间的两个字母“bb”为中心的最大回文子串的长度就是 5 - 1 = 4；

如何计算回文字符子串的总个数？

回到本题，那么我们知道回文子串的长度了，如何计算以某个回文中心为中心有多少个回文子串呢？如果长度为偶数的回文字符串，这个字符串就包含 长度/2 个回文字符串，“abba”中就有“bb”和“abba”两个回文子串。“abccba”中就包含“cc”、“bccb”和“abcba”三个回文子串。同理，长度为奇数的回文字符串中，就包含（长度+1）/2个回文子串。比如“aba”中有“aba”、“a”两个子串。这里我们要注意一个问题，在计算过程中，我们计算的是以这个回文中心为中心的回文子串，比如“aabaa”当计算以‘b’为中心的回文子串的个数的时候两端的‘aa’虽然也构成回文，但他们不是以‘b’为中心的。而他们的会在其他的回文中心被计算。

manacher模板

const int N = 100010;
char S[N];
int cnt[N];

void manacher(string s){
    int l = 0, R = 0, C = 0;
    int n = s.size();
    S[l ++ ] = '$';
    S[l ++ ] = '#';
    for(int i = 0; i < n; i ++ ){
        S[ l ++ ] = s[i];
        S[ l ++ ] = '#';
    }
    S[l] = 0;
    for(int i = 1; i < l; i ++ ){
        cnt[i] = R > i ? min(R - i, cnt[2*C - i]) : 1;
        while(i - cnt[i] > 0 && i + cnt[i] < l)
            if(S[i - cnt[i]] == S[i + cnt[i]]) cnt[i] ++ ;
            else break;
        if(i + cnt[i] > R){
            R = cnt[i] + i;
            C = i;
        }
    }

    return ;
}

本题C++ 代码

class Solution {
public:
    static const int N = 1010, M = 2*N;
    char S[M];
    int cnt[M];
    int countSubstrings(string s) {
        int l = 0, R = 0, C = 0;
        int n = s.size();
        S[l ++ ] = '$';
        S[l ++ ] = '#';
        for(int i = 0; i < n; i ++ ){
            S[l ++ ] = s[i];
            S[l ++ ] = '#';
        }
        S[l] = 0;
        int res = 0;
        for(int i = 1; i < l; i ++ ){
            cnt[i] = R > i ? min(R - i, cnt[2 * C - i]) : 1;
            while(i - cnt[i] > 0 && i + cnt[i] < l)
                if(S[i - cnt[i]] == S[i + cnt[i]]) cnt[i] ++ ;
                else break;
            if(i + cnt[i] > R){
                R = i + cnt[i];
                C = i;
            }
            if(S[i] == '#') res += (cnt[i] - 1) / 2;//以两个字母为回文中心 (长度)/ 2
            else res += cnt[i] / 2;             //以一个字母为回文中心(长度 + 1) / 2
        }
        return res;
    }
};