Prim算法求最小生成树

最小生成树问题概述

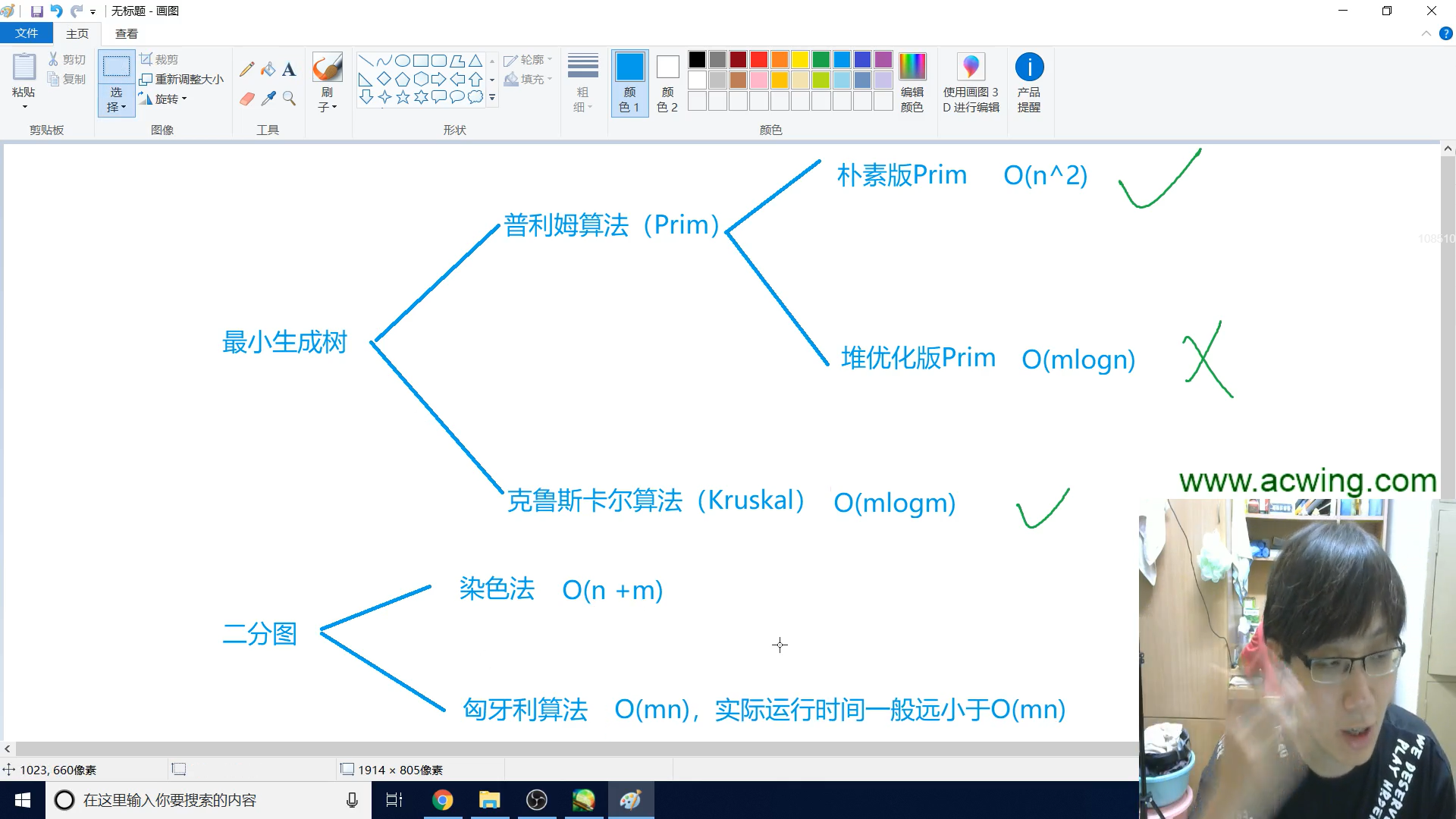
稠密图用朴素$prim$算法，$O(n ^ 2)

稀疏图用$kruskal$，$O(m log n)$

堆优化$prim$也适用于稀疏图，但是近乎全面劣于$kruskal$，所以一般不用

$prim$算法概述

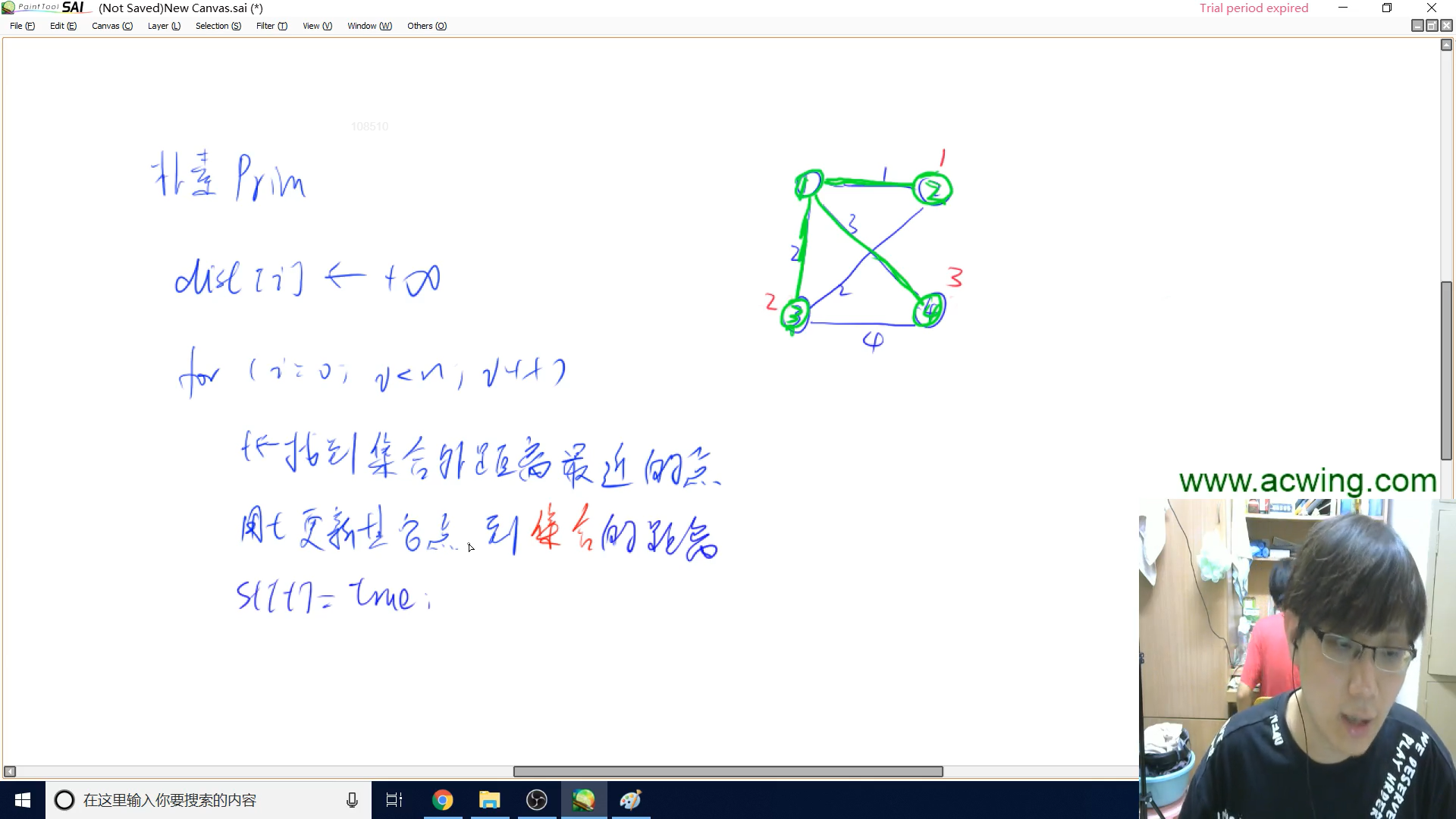
当前集合$S$：在当前生成树的所有点

我们每次将集合外距离集合最近的点，加入到集合里面（将对应的距离最小的边纳入生成树），并且借此更新其他点到集合的最近距离，直到集合内存在连通块的所有点。

如果连通块点总个数和图的总个数相同，那么说明存在最小生成树。反之不存在最小生成树

图的存储

由于是稠密图，选用邻接矩阵

重边选取最小边
自环是不可能出现在最小生成树里的，所以自环直接默认不存在，初始化为无穷

堆优化

该代码与$dijkstra$的优化思路相同，可以仿照着写

代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n;      // n表示点数
int g[N][N];        // 邻接矩阵，存储所有边
int dist[N];        // 存储其他点到当前最小生成树的距离
bool st[N];     // 存储每个点是否已经在生成树中


// 如果图不连通，则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
    memset(dist, 0x3f, sizeof dist); // dist初始化为正无穷

    int res = 0;
    for (int i = 0; i < n; i ++ )
    /* dijkstra是n - 1，是因为找到剩一个点时候，它不需要在计算了。而这里的n，
    最后剩一个点的时候，答案还是要加入边的，所以最后一个点必须实实在在的计算
    一遍所以迭代n次*/
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        if (i && dist[t] == INF) return INF; // 如果是第一次，那么肯定是无穷，此时不应该返回无穷

        if (i) res += dist[t]; // 不是第一次，就把这条边加进去。第一次是不存在边的，不应该计算
        st[t] = true; // 标记下该点已经到达

        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]); // 更新其他点到集合的最短距离
    }

    return res; // 返回最小生成树的边权重之和
}


int main()
{
    scanf("%d%d", &n, &m);

    memset(g, 0x3f, sizeof g); // 图的初始化

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    int t = prim();

    if (t == INF) puts("impossible"); // 不存在生成树就输出 impossible，反之输出答案
    else printf("%d\n", t);

    return 0;
}