算法分析

此题是石子合并的扩展版

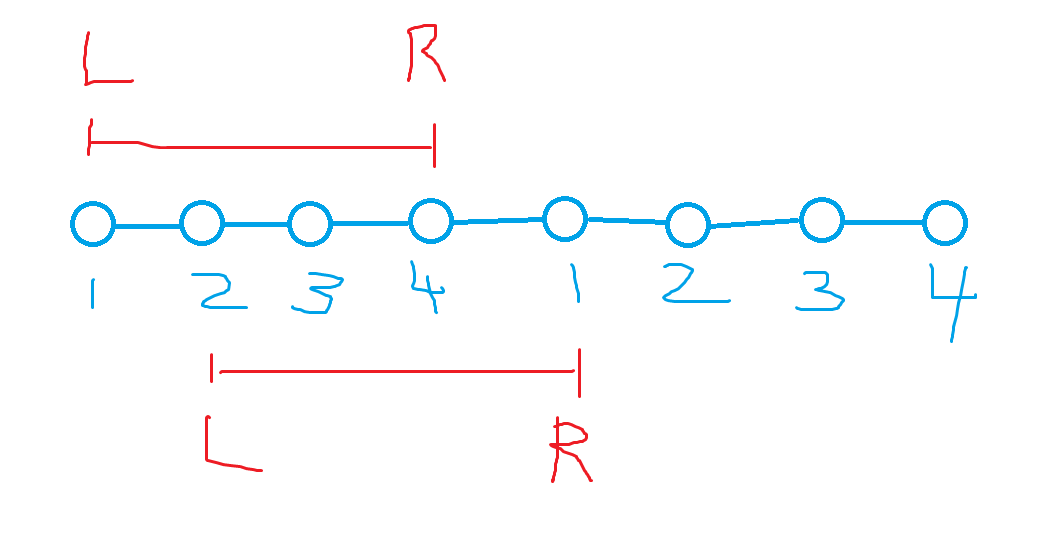
• 1、如图所示，将链形的1到n的石子通过复制加长到两倍，以达到将环形石子拆分成不同情况且长度为n的链形石子的效果

• 2、求所有区间长度为n的链形石子合并

时间复杂度 $O(8n^3)$

参考文献

算法提高课

Java 代码

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main {
    static int N = 410;
    static int n;
    static int[] w = new int[N];
    static int[] s = new int[N];
    static int INF = 0x3f3f3f3f;
    static int[][] f = new int[N][N];
    static int[][] g = new int[N][N];
    public static void main(String[] args)  {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        for(int i = 1;i <= n;i++)
        {
            int x = scan.nextInt();
            w[i] = x;
            w[i + n] = x;   
        }
        //前缀和
        for(int i = 1;i <= n * 2;i++) s[i] = s[i - 1] + w[i];

        for(int len = 2;len <= n;len ++)
            for(int L = 1;L + len - 1 <= n * 2;L ++)
            {
                int R = L + len - 1;
                f[L][R] = INF;
                g[L][R] = -INF;
                for(int k = L;k < R;k++)
                {
                    f[L][R] = Math.min(f[L][R], f[L][k] + f[k + 1][R] + s[R] - s[L - 1]);
                    g[L][R] = Math.max(g[L][R], g[L][k] + g[k + 1][R] + s[R] - s[L - 1]);
                }
            }
        int minv = INF , maxv = -INF;
        for(int i = 1; i <= n;i++)
        {
            minv = Math.min(minv, f[i][i + n - 1]);
            maxv = Math.max(maxv, g[i][i + n - 1]);
        }
        System.out.println(minv);
        System.out.println(maxv);
    }
}