找两个点的距离，只要知道两点的坐标即可。点的坐标如何确定呢？
举例来分析此题，在二级城镇中找 7的坐标。
我们可以从一级城镇的3坐标推出。具体如下。

从图1和图2关系我们做如下分析

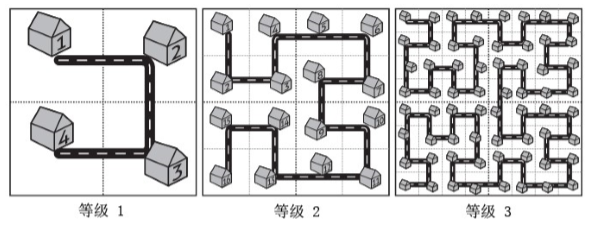
假设图1 的小区 1 2 3 4 为（0，0） （0，1） （1，1） （1，0）
即按数组下标方式组织位置坐标，也是坐标系只不过有方向改变，不影响距离。

图2 由4个图1 组成。
第二个区域 4 5 6 7 为 （0，2） （0，3）（1，3）（1，2）
为图一平移而来，（x2,y2) =(x1,y1+len) len = 2 为图一的边长

len 如何计算呢？ 图一 2 图二 4 图三 8 推图四 16 … len= 2^n

第一个区域 1 2 3 4 为 (0,0) (1,0) (1，1) （0，1）
不难看出，图2 第一区域为图一变换而来，（x2,y2)=(y1,x1)
向图3扩展，发现图3第一区域与图2 的关系得以验证。

第三区域 9 10 11 12 为（2，2）（2，3） （3，3）（3，2）
为图一平移而来，（x2,y2) =(x1+len,y1+len) len = 2 为图一的边长

第四区域 13 14 15 16 为(3,1) (2,1) (2,0) (3,0)
与图一关系为 先将图一逆时针旋转90度 （-y,x）,然后按左右反转，(-y,-x) ---->以数组坐标系左右转变的是y
然后向右平移len，再向左平移1位。
然后向下平移2len，再向上平移1位 （x2,y2) =(2len-1-y1,len-1-x1);

回头看 图二的7 相当于图一的3 平移到第二区域（1，1+len）=(1,3);
由此我们将求第N个等级城镇的A区坐标转为求N-1城镇A对应位置坐标然后平移。
A在N中哪个区域呢？cnt(n) = N城镇的房子总数2^(2N)， A在A/cnt(n-1);
A在N-1城镇如何对应的呢？图3的63，在图2的15，在图一的3。即，A在n-1城镇的 A%cnt。

递归关系已经出现，我们构建递归函数 求第n级别城镇A的坐标

#include<iostream>
#include<cmath>
using namespace std;

typedef long long LL;
typedef pair<LL,LL> PLL;
/*
计算第n级别城镇，m的坐标
*/
PLL calc(LL n,LL m)
{
    if(n==0) return {0,0};
    LL len = 1ll << (n - 1), cnt = 1ll << (2 *(n-1));//len第n-1城镇的边长  cnt第n-1城镇的小区总数
    PLL pos  = calc(n-1,m%cnt);//计算第n-1级别城镇中，对应m点的坐标
    LL x = pos.first, y = pos.second;
    LL z = m / cnt;
    if (z == 0) return {y, x};  //第一区域
    if (z == 1) return {x, y + len};//第二区域
    if (z == 2) return {x + len, y + len};//第三区域
    return {len * 2 - 1 - y, len - x - 1};//第四区域
}

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        LL N,A,B;
        cin>>N>>A>>B;
        PLL ac = calc(N,A-1);
        PLL bc = calc(N,B-1);
        double x = ac.first - bc.first, y = ac.second - bc.second;
        printf("%.0lf\n", sqrt(x * x + y * y) * 10);
    }
    return 0;
}