题目描述

二分图匹配，要求匹配边之间没有相交。

样例

5
-42 58
44 86
7 28
99 34
-13 -59
-47 -44
86 74
68 -75
-68 60
99 -60

4
2
1
5
3

算法1

(二分图KM算法) $O(n^3)$

怎样转化成最大（最小）带权匹配呢？？？

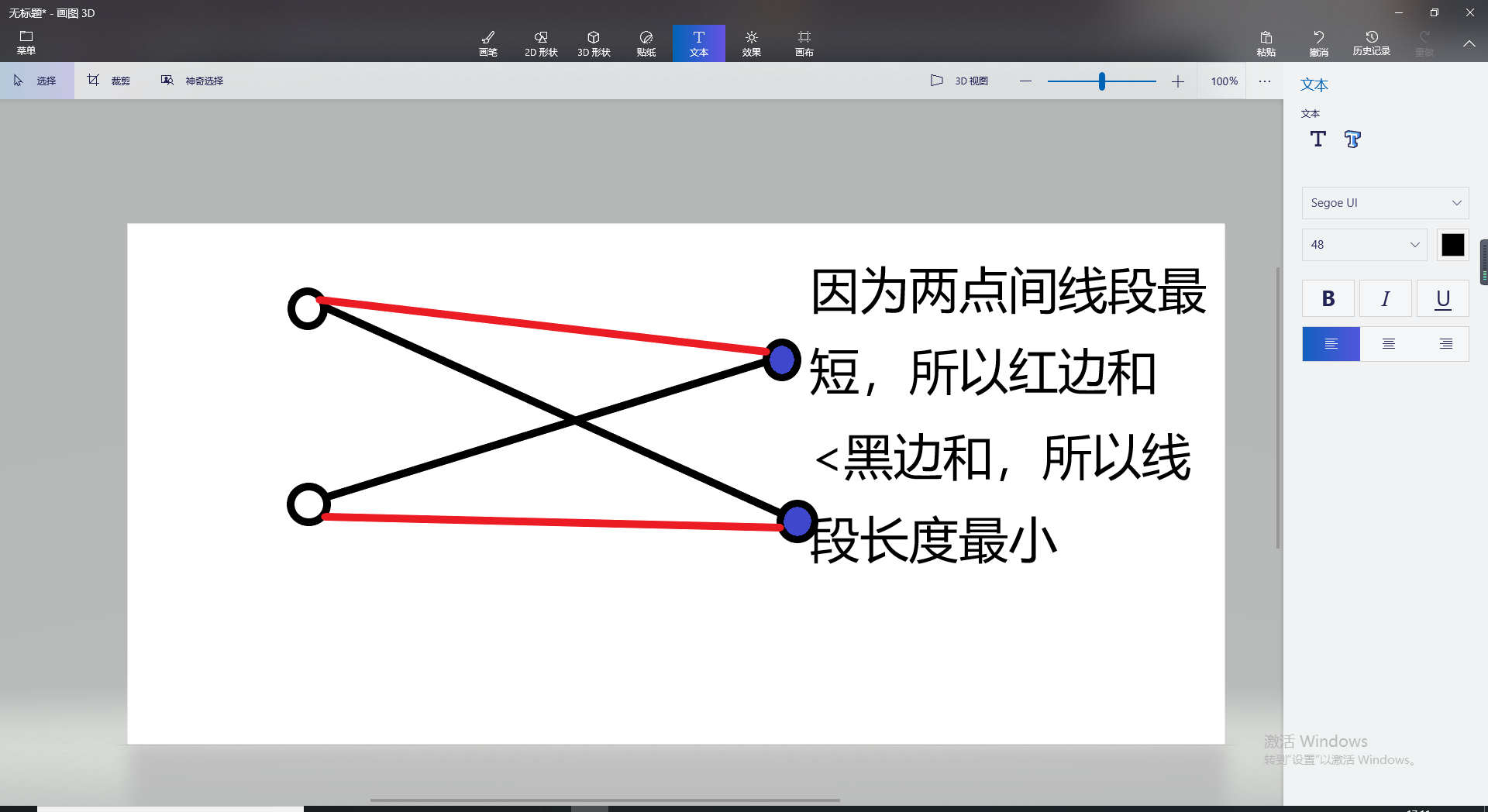
所以该问题便转化为使得匹配边权值之和最小

注意事项：
1·如果是double类型的数据，判断是否为零需要if(fabs(cnt)<1e-10).
2·不直接使用del的原因是会TLE，所以需要用if(va[i]&&!vb[j])剪枝.
4·计算时转换成double类型可以使用number*1.0.

时间复杂度

O(n^3)

C++ 代码

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
inline int read()
{
    int s=0,w=1;
    char c=getchar();
    while(c<'0'||c>'9')
    {
        if(c=='-')
            w=-w;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        s=s*10+c-'0';
        c=getchar();
    }
    return s*w;
}
const int N=100+5;
int n;
struct Node{
    int x,y;
};
Node a[N],b[N];
double mp[N][N];
double la[N],lb[N];
bool va[N],vb[N];
int match[N],ans[N];
double del;
inline double solve_num(int i,int j)
{
    return -sqrt((b[j].x-a[i].x)*(b[j].x-a[i].x)*1.0+(b[j].y-a[i].y)*(b[j].y-a[i].y)*1.0);
}
inline bool dfs(int x)
{
    va[x]=1;
    for(int y=1;y<=n;y++)
    {
        if(vb[y])
            continue;
        double cnt=la[x]+lb[y]-mp[x][y];
        if(fabs(cnt)<1e-10)
        {
            vb[y]=1;
            if(!match[y]||dfs(match[y]))
            {
                match[y]=x;
                return 1;
            }
        }
    }
    return 0;
}
void KM()
{
    for(int i=1;i<=n;i++)
    {
        la[i]=-(1<<30);
        lb[i]=0;
        for(int j=1;j<=n;j++)
            la[i]=max(la[i],mp[i][j]);
    }
    for(int x=1;x<=n;x++)
    {
        while(1)
        {
            memset(va,0,sizeof(va));
            memset(vb,0,sizeof(vb));
            if(dfs(x))
                break;
            del=1<<30;
            for(int i=1;i<=n;i++)
                if(va[i])
                    for(int j=1;j<=n;j++)
                    {
                        if(!vb[j])
                            del=min(del,la[i]+lb[j]-mp[i][j]);
                    }
            for(int i=1;i<=n;i++)
            {
                if(va[i])
                    la[i]-=del;
                if(vb[i])
                    lb[i]+=del;
            }
        }
    }
    for(int y=1;y<=n;y++)
    {
        ans[match[y]]=y;
    }
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        a[i].x=read();
        a[i].y=read();
    }
    for(int i=1;i<=n;i++)
    {
        b[i].x=read();
        b[i].y=read();
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            mp[i][j]=solve_num(i,j);
    KM();
    for(int i=1;i<=n;i++)
        printf("%d\n",ans[i]);
    return 0;
}