有边数限制的最短路

$Bellman-Ford$概述

$bellman-ford$算法对边的存储没有要求，只要能遍历到每个边就行，所以我们可以用最傻瓜式的结构体来存储边。

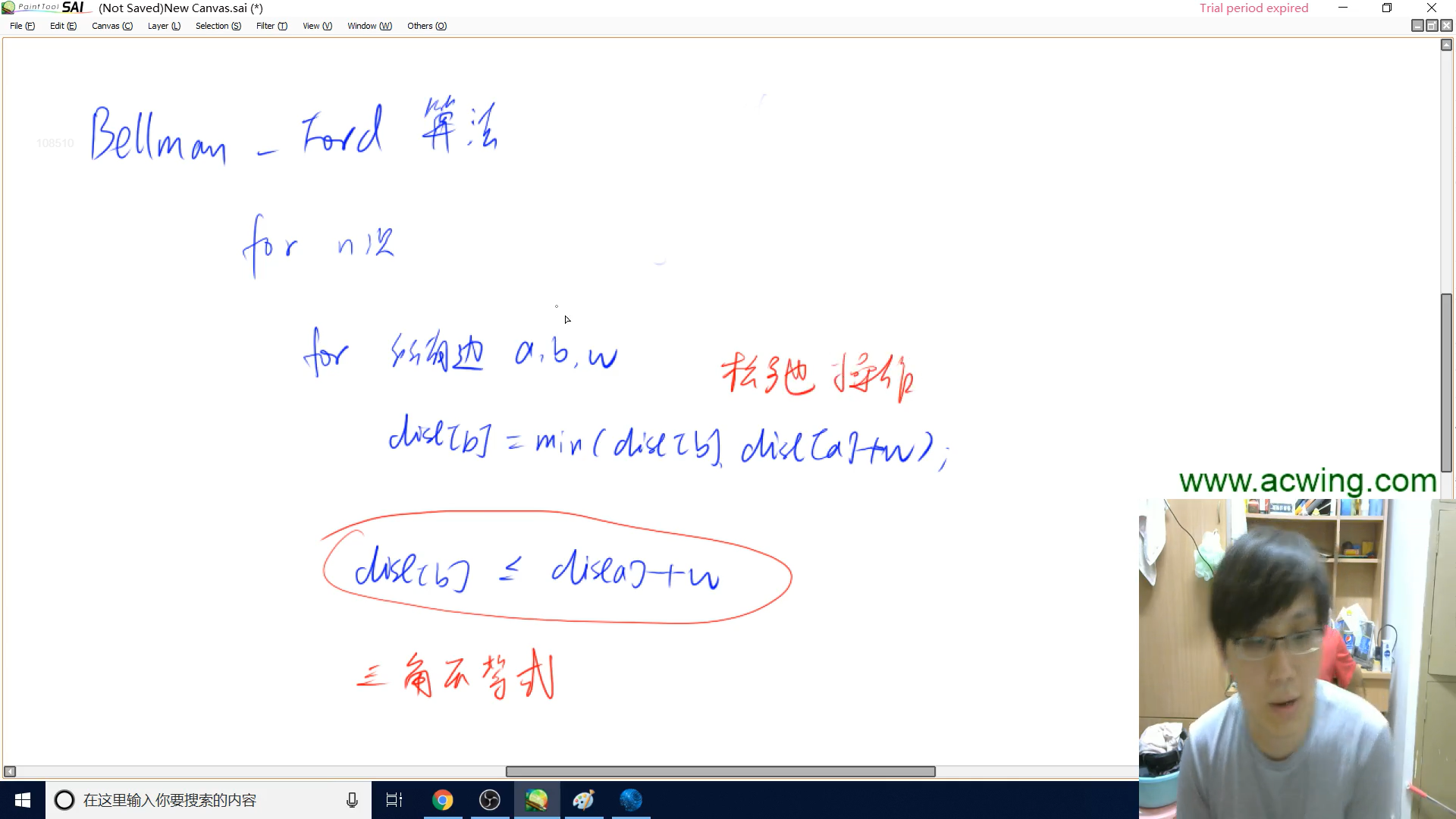
遍历到边后进行松弛操作

在n此迭代内，对每一个边{a, b, w}
dist[b] = min(dist[b], dist[a] + w)

修改数据的串联问题

由于我们修改$dist$数组可能会出现串联问题(串联不会导致最短路结果出现差错，但是会让迭代失去意义，第一次串联意味着某一个点的最短距离经过的边数要多于别的点一条)，所以我们每次需要对上一次得到的$dist$进行一次备份，每次拿备份来进行额更新，这里可以使用$memcpy$函数进行备份

结果判断

由于边存在负值，并且我们会遍历所有的边进行更新（哪怕它是不可达的），这里更新时候会计算不可达的点，所以我们最后判断可达与不可达不再是等于无穷了，因为在计算机中它是一个存储的具体值，一亿减一，这也是不可达，但它的值不是一亿了。所以要通过与一个很大的数来比较，判断是否可以到达

n次迭代的意义

表示经过不超过$n$条边的最短距离，即可以限制通过边的条数，这是其它最短路算法没有的特性

如果存在负权回路，它的最短距离是不一定存在的，我们可以借助这个意义来判断是否存在负环。依旧是如果它的最短距离中间总共经过了$n$条边，那么由抽屉原理得，必然经过$n + 1$个点，所以一定存在负权回路

时间复杂度

$n$次迭代，每次$m$次取最小，所以是$O(nm)$的

本题思路分析

由于题目限制了边的条数，所以只能用$bellman-ford$算法，迭代$k$次即可得到答案

代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, M = 10010;

struct Edge // 边的存储
{
    int a, b, c;
}edges[M];

int n, m, k;
int dist[N]; // 最短路数组
int last[N]; // 备份数组

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist); // 初始化

    dist[1] = 0;
    for (int i = 0; i < k; i ++ ) // 经过不少于k条边的最短路
    {
        memcpy(last, dist, sizeof dist); // 每次将dist备份到last数组，防止串行问题
        for (int j = 0; j < m; j ++ ) // 松弛操作
        {
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.c); // 松弛操作
        }
    }
}

int main()
{
    scanf("%d%d%d", &n, &m, &k);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c}; // 存边
    }

    bellman_ford();

    if (dist[n] > 0x3f3f3f3f / 2) puts("impossible"); // 判断该点是否可达
    else printf("%d\n", dist[n]);

    return 0;
}