Dijkstra求最短路 II

堆优化$dijkstra$概述

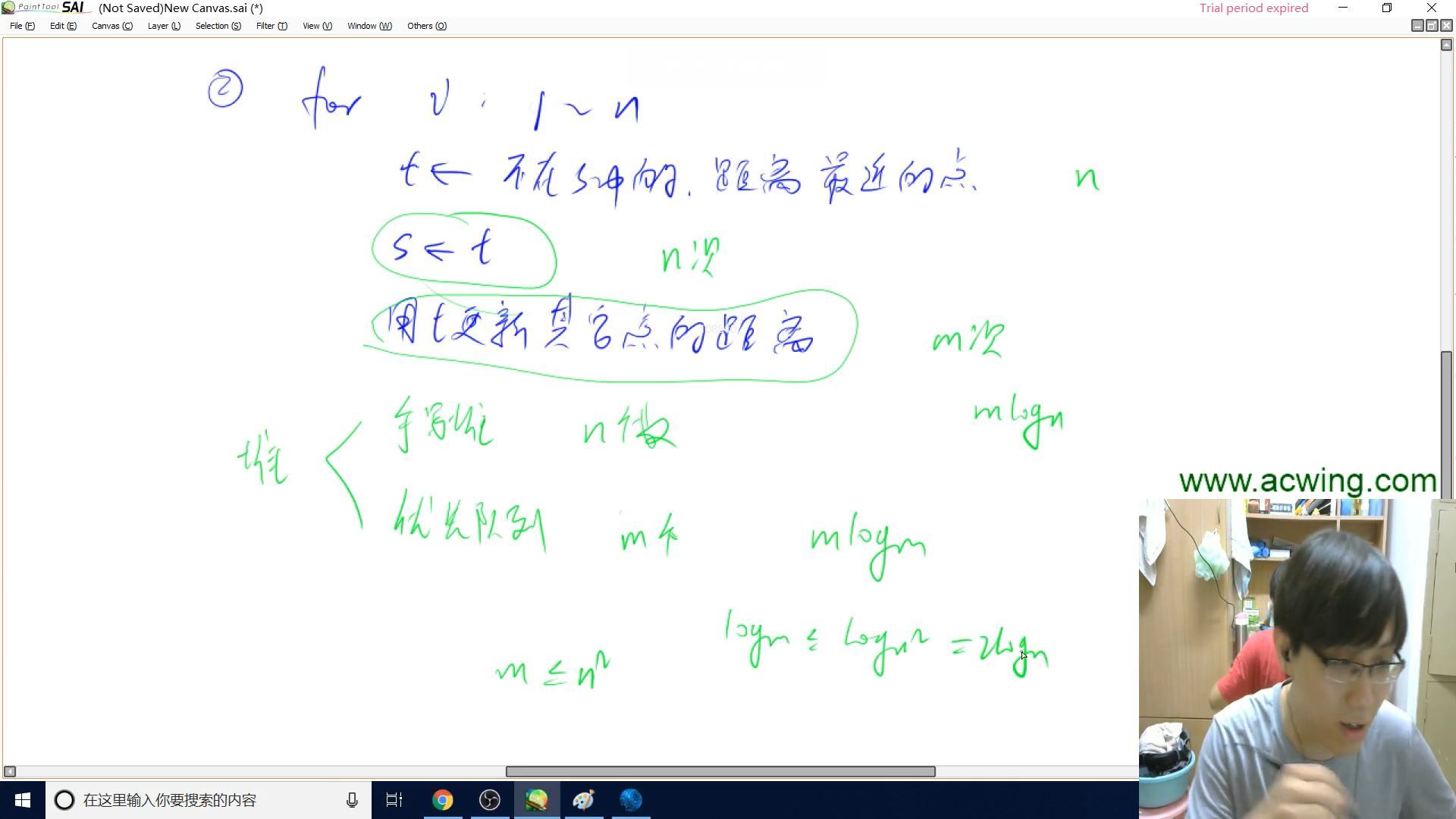
原理

分析朴素$dijkstra$可以发现，其中最影响速度的一步是寻找$dist$[ ]中最小值，这一步是$O(n)$的。我们如果采用堆，那么这一步将会是$O(1)$的，不过后面由此点更新到其他结点的距离那一步骤总次数将会由$m$次变$mlongn$次

适用性与时间复杂度

如果图是稀疏图$m$ ~ $n$，那么很明显$mlongn$更加优秀。而稠密图堆优化后则为$n^2 logn$,反而不如之前

堆的使用与堆内数据存储

这里堆是小根堆，可以采用$stl$内的优先队列，不过默认的是大根堆，所以我们要自己声明小根堆priority_queue<PII, vector<PII>, greater<PII>> heap; 对组里面存的是$pair$，第一个关键字存的是值，第二个关键字存的是顶点序号

对于已经在确定过最小值的点，过滤掉就行

我们是要对在$dist$[ ]中的值排序，所以值是第一关键字（pair是第一关键字先比，然后再看第二关键字）。当然你也可以自己手写结构体并且重载运算符

图的存储

堆优化使用稀疏图，所以这里采用邻接表的存储模式,邻接表需要额外维护权值信息，增加一个权重数组就行

代码

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

typedef pair<int, int> PII; // 堆内元素用pair存储

const int N = 1e6 + 10;

int n, m;
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储
int dist[N]; // 最短路数组
bool st[N];

void add(int a, int b, int c) // 维护边权的邻接表的添加操作
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist); // 初始化
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap; // 堆的声明
    heap.push({0, 1}); // 距离为0，结点编号为1

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first; // ver是结点编号，distance为距离

        if (st[ver]) continue; // 如果该点的最短距离已经确定就过滤
        st[ver] = true; // 没有确定，那么现在已经确定

        for (int i = h[ver]; i != -1; i = ne[i]) // 根据该点临边更新别的点的最短距离
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}