Dijkstra求最短路 I

最短路问题概述

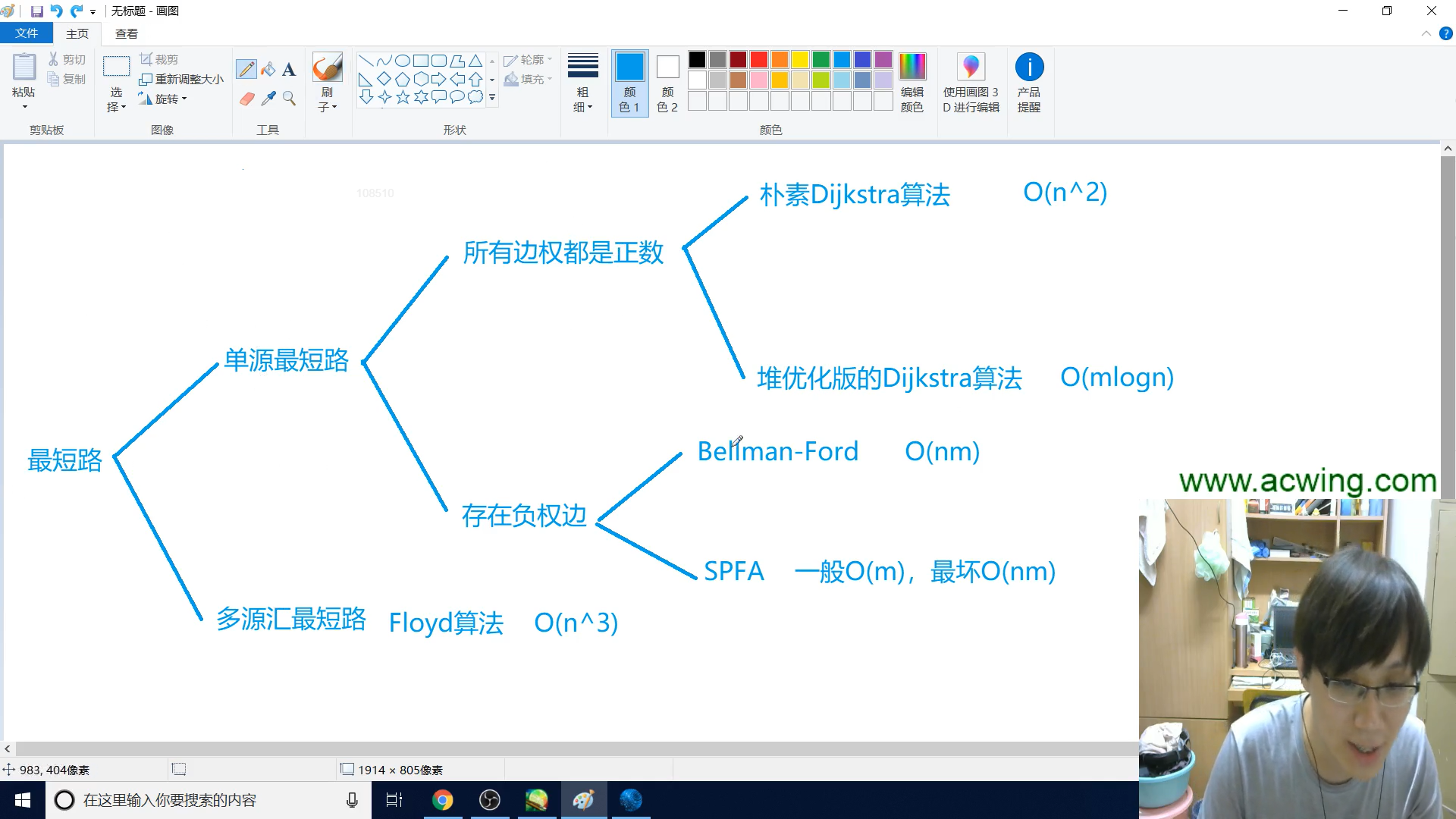
如上图所示

最短路问题可以分成两类
1. 单源最短路
2. 多源汇最短路

$n$为图中所有顶点的个数, $m$为所有边的个数

1. 单源最短路

(1) 所有边为正数或0

1. 朴素$dijkstra$, $O(n^2)$， 适合稠密图
2. 堆优化$dijkstra$, $O(mlogn)$， 适合稀疏图

(2) 边权含负值

1. $bellman$-$ford$, $(nm)$， 如果限制经过的边数，只能用这个算法
2. $spfa$，最坏$O(nm)$，一般会远快于这个下线， 不过它也很容易被卡掉

2. 多源汇最短路

$floyd$算法， $O(n^3)$

我们在思考最短路问题时候，只考虑有向图，无向图是特殊的有向图

稀疏图: $m$ ~ $n$
稠密图：$m$ ~ $n ^ 2$

本部分内容重点在于建模，而不是证明，牢记每个算法的流程与使用条件、时间复杂度

朴素dijkstra概述

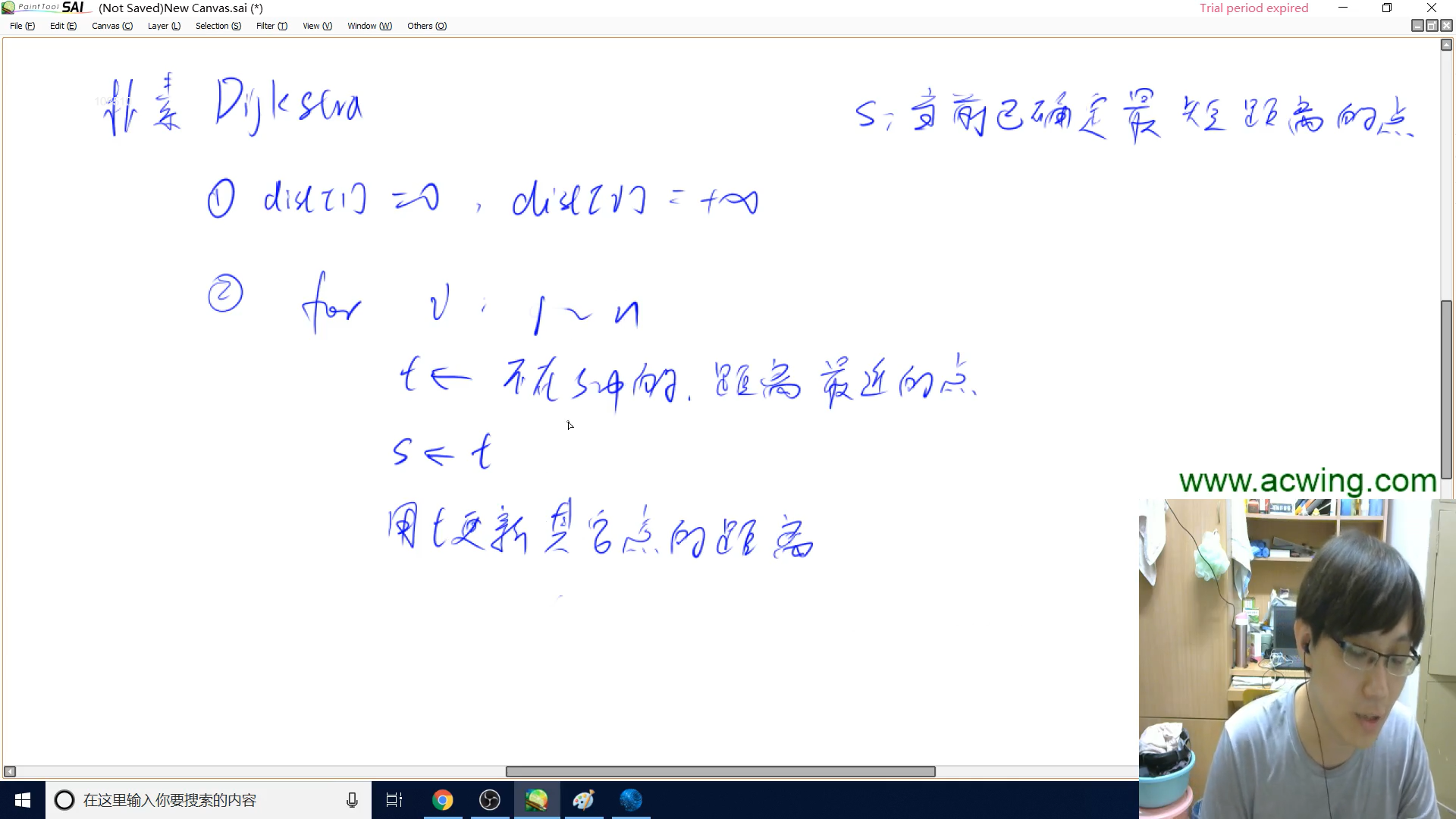
1. 确定初始结点

将它到自己的距离设置为$0$，它到别的结点的距离初始化为正无穷

    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

2. 依次将别的点加入已经确定最短距离的点的集合

$(1)$ 首先找出目前未确定最短距离的，并且距离最短的点
刚开始集合外有$n$个点，但是确认了$n - 1$个点后，最后一个点是不会再更新其它的点的，所以循环$n - 1$次（我习惯写$n$次，因为每次确认一个点，一次迭代也不会浪费多少时间）

    int t = -1;
    for (int j = 1; j <= n; j ++ )
        if (!st[j] && (t == -1 || dist[t] > dist[j]))
        t = j;

$(2)$ 将它纳入集合，并且更新集合外点到集合内的距离

    st[j] = true;
    for (int j = 1; j <= n; j ++ )
        dist[j] = min(dist[j], dist[t] + g[t][j]);

本题思路分析

算法整体思路如上，不过初始化是需要考虑一下的

本题含有重边和自环，这里自环一定会增加长度，所以舍去；重边则取边权值最小的

代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510; // 定点数

int n, m;
int g[N][N]; // 图
int dist[N]; // 最短距离数组
bool st[N]; // 已经确定最小值的集合

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist); 
    dist[1] = 0; // 初始化dist数组，并选择起点

    for (int i = 0; i < n - 1; i ++ )
    /* 每次将一个点加入确定最小值得集合，有n个点所以按理说应该是迭代n次。
    不过只剩一个点时候，前面的都已经确定最短距离了，它只需要直接加入，而无需更新。
    所以最后一次可以省略，写作n - 1也是可以的 */
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ ) // 找出dist[ ] 最小值的下标
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        for (int j = 1; j <= n; j ++ ) // 用最小值的点，依次更新别的点最小距离
            dist[j] = min(dist[j], dist[t] + g[t][j]);

        st[t] = true; // 将该点纳入确定最小值的集合
    }

    if (dist[n] == 0x3f3f3f3f) return -1; // 由于边没有负数，所以可以取等
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(g, 0x3f, sizeof g); // 初始化图
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);

        g[a][b] = min(g[a][b], c); // 重边取最短的那条
    }

    printf("%d\n", dijkstra());

    return 0;
}