算法提高课汇总

算法思路

理解题意

在AcWing 282. 石子合并基础上允许以环形的形式合并石子.

将环形问题转为线性问题的简洁思路: 重复所有线性石子接在原$N$个石子后面即可.

因为环形的本质是我们可以任意以某个石子作为线性起点. 以4个石子为例:

可以环形合并4个石子等价于考虑4种线性情况:

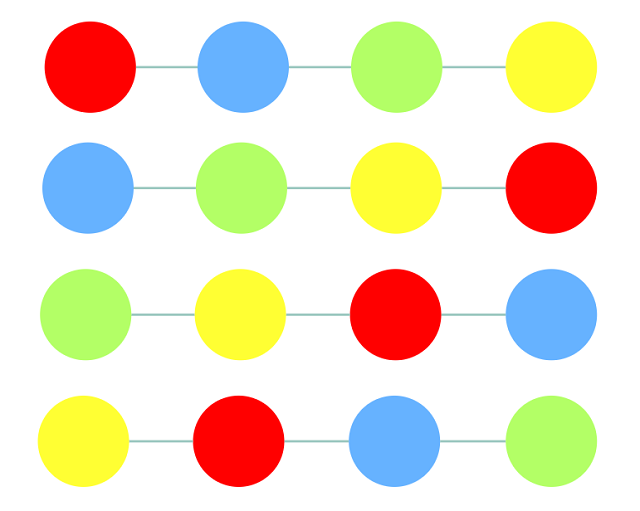
而用我们上述思路可以实现相同效果:

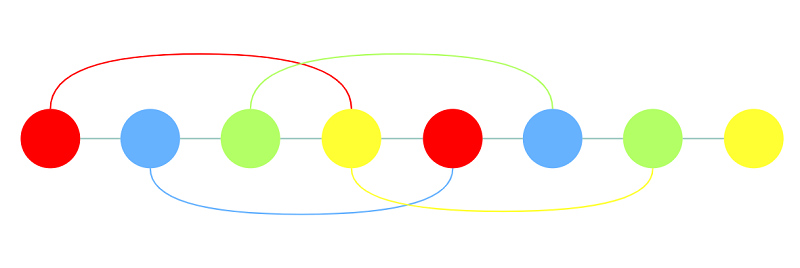
代码实现

#include <cstring>
#include <iostream>

using namespace std;

const int N = 410, INF = 0x3f3f3f3f;

int n;
int w[N], s[N];
int f[N][N], g[N][N]; //分别计算最小值和最大值

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )
    {
        cin >> w[i];
        w[i + n] = w[i]; //赋值一份
    }
    for( int i = 1; i <= 2 * n; i ++ )  s[i] = w[i] + s[i - 1];

    memset(f, 0x3f, sizeof f);
    for( int i = 1; i <= 2 * n; i ++ )  f[i][i] = 0;

    for( int len = 2; len <= n; len ++ )
    {
        for( int i = 1; i + len - 1 <= 2 * n; i ++ )
        {
            int j = i + len - 1;
            for( int k = i; k < j; k ++ )
            {
                f[i][j] = min( f[i][j], f[i][k] + f[k + 1][j] );
                g[i][j] = max( g[i][j], g[i][k] + g[k + 1][j] );
            }
            f[i][j] += s[j] - s[i - 1];
            g[i][j] += s[j] - s[i - 1];
        }
    }

    int maxv = -INF, minv = INF;
    for( int i = 1; i <= n; i ++ )
    {
        minv = min( minv, f[i][i + n - 1]);
        maxv = max( maxv, g[i][i + n - 1]);
    }
    cout << minv << endl << maxv << endl;

    return 0;
}